
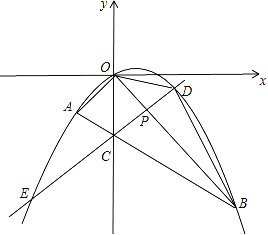
【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.
(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
【答案】(1)y=![]() ,y=-x;(2)
,y=-x;(2)![]() ;(3)△BOD的面积有最大值,最大值为
;(3)△BOD的面积有最大值,最大值为![]() ,D(
,D(![]() ).
).
【解析】试题分析:(1)首先解方程得出A,B两点的坐标,利用待定系数法确定直线AB和直线OB的解析式即可;
(2)利用待定系数法求出二次函数解析式即可;
(3)利用S△BOD=S△ODQ+S△BDQ得出关于x的二次函数,进而得出最值即可.
解:(1)解方程x2-2x-3=0,
得 x1=3,x2=-1.
∵m<n,
∴m=-1,n=3,
∴A(-1,-1),B(3,-3).
设直线AB的解析式为y=kx+b
∴![]() ,
,
解得: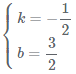 .
.
∴直线AB的解析式为y=-![]() x+
x+![]() ;
;
设直线OB的解析式为y=kx,
∴3k=-3,
解得:k=-1,
∴直线OB的解析式为y=-x;
(2)∵抛物线过原点,设抛物线的解析式为y=ax2+bx(a≠0).
∴![]() ,
,
解得: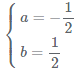 ,
,
∴抛物线的解析式为y=-![]() x2+
x2+![]() x.
x.
(3)△BOD的面积是存在最大值;
过点D作DG⊥x轴,垂足为G,交OB于Q,过B作BH⊥x轴,垂足为H.
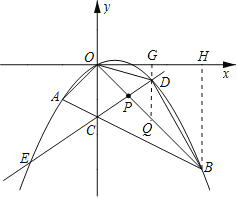
设Q(x,-x),D(x,-![]() x2+
x2+![]() x).
x).
S△BOD=S△ODQ+S△BDQ=12DQOG+12DQGH,
=![]() DQ(OG+GH),
DQ(OG+GH),
=![]() [x+(-
[x+(-![]() x2+
x2+![]() x)]×3,
x)]×3,
=-![]() (x-
(x-![]() )2+
)2+![]() ,
,
∵0<x<3,
∴当x=![]() 时,S取得最x大值为
时,S取得最x大值为![]() ,此时D(
,此时D(![]() ,-
,-![]() ).
).


科目:初中数学 来源: 题型:
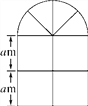
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了进一步改善环境,郑州市今年增加了绿色自行车的数量,已知A型号的自行车比B型号的自行车的单价低30元,买8辆A型号的自行车与买7辆B型号的自行车所花费用相同.
(1)A,B两种型号的自行车的单价分别是多少?
(2)若购买A,B两种自行车共600辆,且A型号自行车的数量不多于B型号自行车的一半,请你给出一种最省钱的方案,并求出该方案所需要的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用分式方程解决问题:元旦假期有两个小组去攀登- -座高h米的山,第二组的攀登速度是第- -组的a倍.
(1)若![]() ,两小组同时开始攀登,结果第二组比第一组早
,两小组同时开始攀登,结果第二组比第一组早![]() 到达顶峰.求两个小组的攀登速度.
到达顶峰.求两个小组的攀登速度.
(2)若第二组比第一组晚出发![]() ,结果两组同时到达顶峰,求第二组的攀登速度比第一组快多少? (用含
,结果两组同时到达顶峰,求第二组的攀登速度比第一组快多少? (用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳泉市郊区教科局提出开展“三有课堂”,某中学在一节体现“三有课堂”公开展示课上,李老师展示一幅图,条件是:C为直线AB上一点,∠DCE为直角,CF平分∠ACD,CH平分∠BCD,CG平分∠BCE,各个小组经过讨论后得到以下结论:①∠ACF与∠BCH互余 ②∠FCG与∠HCG互补 ③∠ECF与∠GCH互补 ④∠ACD﹣∠BCE=90°,聪明的你认为哪些组的结论是正确的,正确的有( )个.
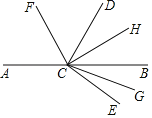
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】郊区某中学学霸父母只要有时间就陪孩子一起完成家庭作业,在某天晚上,勤芬准备完成作业时:化简(![]() x2+7x+6)﹣(7x+8x2﹣4).发现系数“
x2+7x+6)﹣(7x+8x2﹣4).发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)她把“![]() ”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
”猜成3,请你化简:(3x2+7x+6)﹣(7x+8x2﹣4);
(2)爸爸说:“你猜错了,我看了标准答案的结果是常数.”请你通过计算说明来帮助勤芬得到原题中“![]() ”是几.
”是几.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,a)是反比例函数![]() 的图象上一点,直线
的图象上一点,直线![]() 与反比例函数
与反比例函数![]() 的图象在第四象限的交点为点B.
的图象在第四象限的交点为点B.
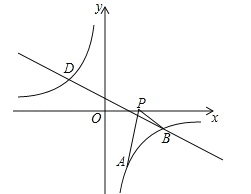
(1)求直线AB的解析式;
(2)动点P(x,0)在x轴的正半轴上运动,当线段PA与线段PB之差达到最大时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
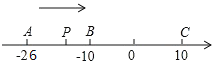
【题目】已知数轴上有A、B、C三点,分别表示有理数﹣26,﹣10,10,动点P从A出发,以每秒1个单位的速度向右移动,当P点运动到C点时运动停止,设点P移动时间为t秒。
(1)用含t的代数式表示P到点A和点C的距离:PA=_____,PC=_____.
(2)当点P运动到B点时,点Q从A出发,以每秒3个单位的速度向右运动,求t等于多少秒时P、Q两点相遇?t等于多少秒时P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
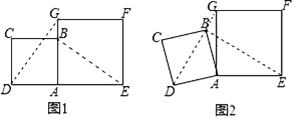
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com