
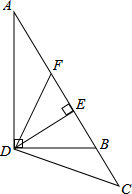
 在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE=
在△ABD中,∠ADB=90°,DE⊥AB于E,过AB的中点F作DF⊥CD交AB延长线于C.若BE=| 1 |
| 5 |
| 5 |
| 2 |
 解:如图,∵BE=
解:如图,∵BE=| 1 |
| 5 |
| 5 |
| 2 |
| 5λ |
| 2 |
| 5λ |
| 2 |
| 8 |
| 13 |
| 8 |
| 13 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
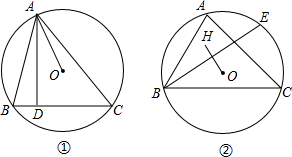 如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.
如图①,小聪在学习圆的性质时发现一个结论,△ABC内接于⊙O,AD⊥BC,则∠BAD=∠OAC.查看答案和解析>>
科目:初中数学 来源: 题型:
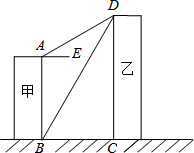 如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD.
如图,线段AB、CD分别表示甲、乙两建筑物的高,AB⊥BC,DC⊥BC,AE∥BC,测得∠DBC=60°,∠DAE=30°,已知甲建筑物高AB=36米.求乙建筑物的高CD.查看答案和解析>>
科目:初中数学 来源: 题型:
 小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明)
小明和小亮用图中的转盘做游戏:分别转动转盘两次,若两次数字之差(大数减小数)等于2,小明胜;若两次数字之差(大数减小数)等于1,则小亮胜,这个游戏对双方公平吗?说说你的理由.(列表或画树状图说明)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图是游乐园的一角.
如图是游乐园的一角.查看答案和解析>>
科目:初中数学 来源: 题型:
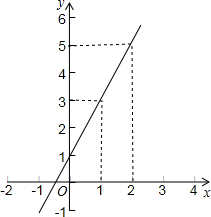 小明认为一次函数y=kx+b中,x每增加1,kx增加了k,b没有变,因此y也增加了k.如图所示的一次函数图象中,x从1变到2时,函数值从3变到5,增加了2,因此该一次函数中k的值是2.请你用待定系数法验证小明的说法.
小明认为一次函数y=kx+b中,x每增加1,kx增加了k,b没有变,因此y也增加了k.如图所示的一次函数图象中,x从1变到2时,函数值从3变到5,增加了2,因此该一次函数中k的值是2.请你用待定系数法验证小明的说法.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com