
【题目】如图,把面积为a的正三角形ABC的各边依次循环延长一倍,顺次连接这三条线段的外端点,这样操作后,可以得到一个新的正三角形DEF;对新三角形重复上述过程,经过2016次操作后,所得正三角形的面积是 . 
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABD中,AB=AD,AO平分∠BAD,过点D作AB的平行线交AO的延长线于点C,连接BC. 
(1)求证:四边形ABCD是菱形;
(2)如果OA,OB(OA>OB)的长(单位:米)是一元二次方程x2﹣7x+12=0的两根,求AB的长以及菱形ABCD的面积;
(3)若动点M从A出发,沿AC以2m/S的速度匀速直线运动到点C,动点N从B出发,沿BD以1m/S的速度匀速直线运动到点D,当M运动到C点时运动停止.若M、N同时出发,问出发几秒钟后,△MON的面积为 ![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y= ![]() (x>0)的图象上.
(x>0)的图象上.
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:
①abc<0;② ![]() >0;③ac﹣b+1=0;④OAOB=﹣
>0;③ac﹣b+1=0;④OAOB=﹣ ![]() .
.
其中正确结论的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC. 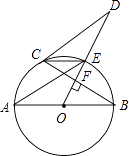
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为强化安全意识,某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练,请完成下列问题:
(1)周三没有被选择的概率;
(2)选择2天恰好为连续两天的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程﹣x2+2ax+2﹣3a=0的一根x1≥1,另一根x2≤﹣1,则抛物线y=﹣x2+2ax+2﹣3a的顶点到x轴距离的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的边AB=4,且BC>AB,一个量角器如图所示放置,其中零刻度(即半圆O的直径)与边AB重合,点A处是0刻度,点B处是180刻度,点P是量角器的半圆弧上一动点,过点P作半圆的切线,设点P的刻度数为m,过点P的切线交线段BC与线段AD于点E,F.
(1)设∠PAB=n.
①如图1,当m=114°时,n=;
②直接写出n与m的关系式:;
(2)试说明AF·BE是否是一个定值,若是,请求出它的值;若不是,请说明理由;
(3)当EF= ![]() 时,求点P的刻度数m的值.
时,求点P的刻度数m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ,EBˊ分别交边AC于点F,G,若∠ADF=80°,则∠EGC的度数为 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com