
【题目】周老师为了了解学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半年的跟踪调查,并将调查结果分成四类A:优;B:良;C:中;D:差.依据调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
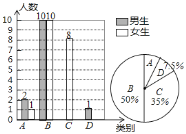
(1)本次调查中,周老师一共调查了______名学生;
(2)将统计图补充完整;
(3)为了共同进步,周老师想从被调查的A类和D类学生中分别选取一位同学进行“一对一”帮扶,请用列表法或画树形图的方法求所选的两位同学恰好是两位女同学的概率.
【答案】(1)40;(2)如图所示:见解析;(3)所选的两位同学恰好是两位女同学的概率为![]() .
.
【解析】
(1)依据B类的学生人数以及百分比即可得到调查的学生人数;
(2)C类的学生人数为40×35%=14(人),其中男生有148=6(人);D类学生人数为40×7.5%=3(人),其中女生有31=2(人);A类学生人数所占的百分比为3÷40=7.5%;据此可将统计图补充完整;
(3)根据树状图可得,共有9种等可能的结果,其中所选的两位同学恰好是两位女同学的情况有2种,即可得到所选的两位同学恰好是两位女同学的概率.
(1)20÷50%=40(人)
故答案为:40;
(2)C类的学生人数为40×35%=14(人),其中男生有14-8=6(人);
D类学生人数为40×7.5%=3(人),其中女生有3-1=2(人);
A类学生人数所占的百分比为3÷40=7.5%;
如图所示:
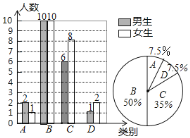
(3)画树状图如下:
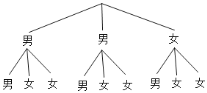
共有9种等可能的结果,其中所选的两位同学恰好是两位女同学的情况有2种,
∴所选的两位同学恰好是两位女同学的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,AB=AC=4,BD=6,P是线段BD上任意一点,过点P作PQ∥AB,与AC交于点Q,设BP=x,PQ=y,则能反映y与x之间关系的图象为( )
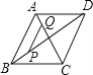
A.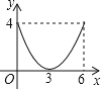 B.
B.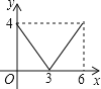 C.
C.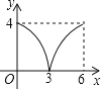 D.
D.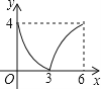
查看答案和解析>>
科目:初中数学 来源: 题型:
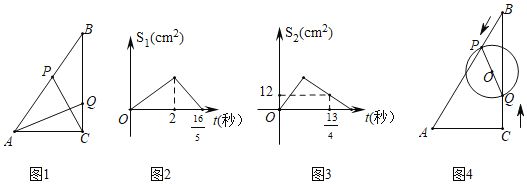
【题目】如图(1),在Rt△ABC中,∠ACB=90°,AC=6cm,动点P从点B出发,沿折线B→A→C路线匀速运动到C停止,动点Q从点C出发,沿折线C→B→A路线匀速运动到A停止,如点P、Q同时出发运动t秒后,如图(2)是△BPC的面积S1(cm2)与t(秒)的函数关系图象,图(3)是△AQC的面积S2(cm2)与t(秒)的函数关系图象:
(1)点P运动速度为 cm/秒;Q运动的速度 cm/秒;
(2)连接PQ,当t为何值时,PQ∥BC;
(3)如图(4)当运动t(0≤t≤2)秒时,是否存在这样的时刻,使以PQ为直径的⊙O与Rt△ABC的一条边相切,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
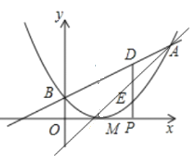
【题目】已知二次函数图象的顶点坐标为![]() ,直线
,直线![]() 与二次函数的图象交于
与二次函数的图象交于![]() ,
,![]() 两点,其中
两点,其中![]() 点的坐标为
点的坐标为![]() ,
,![]() 点在
点在![]() 轴上.
轴上.
(1)求![]() 的值及这个二次函数的解析式;
的值及这个二次函数的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的周长最小,并求出此时
的周长最小,并求出此时![]() 点坐标;
点坐标;
(3)若![]() 是
是![]() 轴上的一个动点,过
轴上的一个动点,过![]() 作
作![]() 轴的垂线分别于直线
轴的垂线分别于直线![]() 和二次函数的图象交于
和二次函数的图象交于![]() ,
,![]() 两点.当
两点.当![]() 时,求线段
时,求线段![]() 的最大值;
的最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
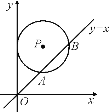
【题目】如图,在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为2![]() ,则a的值是( )
,则a的值是( )
A. 2![]() B. 2+2
B. 2+2![]() C. 2
C. 2![]() D. 2+
D. 2+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少( )个时,网球可以落入桶内.
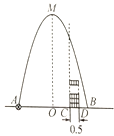
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com