
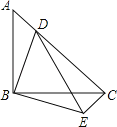
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点D在AC上,将△ABD绕点B顺时针旋转90°后得到△CBE.
(1)求∠DCE的度数;
(2)当AC=4,AD:DC=1:3时,求DE的长.
【答案】(1)90°;(2)![]() .
.
【解析】
(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;
(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.
(1)∵∠ABC=90°,AB=BC,
∴∠A=∠ACB=45°,
∵△CBE是由△ABD旋转得到,
∴∠A=∠BCE=45°,
∴∠DCE=∠ABC+∠BCE=90°;
(2)∵AD:DC=1:3,
设AD=x,CD=3x,
∴x+3x=4,
解得:x=1,
∴AD=CE=1,DC=3,
由勾股定理得:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
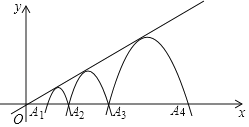
【题目】若二次函数的图象与x轴的两个交点和顶点构成等边三角形,则称这样的二次函数的图象为标准抛物线.如图,自左至右的一组二次函数的图象T1,T2,T3……是标准抛物线,且顶点都在直线y=![]() x上,T1与x轴交于点A1(2,0),A2(A2在A1右侧),T2与x轴交于点A2,A3,T3与x轴交于点A3,A4,……,则抛物线Tn的函数表达式为_____.
x上,T1与x轴交于点A1(2,0),A2(A2在A1右侧),T2与x轴交于点A2,A3,T3与x轴交于点A3,A4,……,则抛物线Tn的函数表达式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践﹣四边形旋转中的数学
“智慧”数学小组在课外数学活动中研究了一个问题,请帮他们解答.
任务一:如图1,在矩形ABCD中,AB=6,AD=8,E,F分别为AB,AD边的中点,四边形AEGF为矩形,连接CG.
(1)请直接写出CG的长是______.
(2)如图2,当矩形AEGF绕点A旋转(比如顺时针旋转)至点G落在边AB上时,请计算DF与CG的长,通过计算,试猜想DF与CG之间的数量关系.
(3)当矩形AEGF绕点A旋转至如图3的位置时,(2)中DF与CG之间的数量关系是否还成立?请说明理由.
任务二:“智慧”数学小组对图形的旋转进行了拓展研究,如图4,在ABCD中,∠B=60°,AB=6,AD=8,E,F分别为AB,AD边的中点,四边形AEGF为平行四边形,连接CG.“智慧”数学小组发现DF与CG仍然存在着特定的数量关系.
(4)如图5,当AEGF绕点A旋转(比如顺时针旋转),其他条件不变时,“智慧”数学小组发现DF与CG仍然存在着这一特定的数量关系.请你直接写出这个特定的数量关系.





查看答案和解析>>
科目:初中数学 来源: 题型:
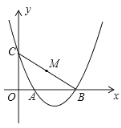
【题目】如图,抛物线![]() 交x轴于点A,B,交y轴于点C,当
交x轴于点A,B,交y轴于点C,当![]() 纸片上的C沿着此抛物线运动时,则
纸片上的C沿着此抛物线运动时,则![]() 纸片随之也跟着水平移动,设纸片上CB的中点M坐标为
纸片随之也跟着水平移动,设纸片上CB的中点M坐标为![]() ,在此运动过程中,n与m的关系式是( )
,在此运动过程中,n与m的关系式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新型高科技商品,每件的售价比进价多6元,5件的进价相当于4件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖5件.
(1)该商品的售价和进价分别是多少元?
(2)设每天的销售利润为w元,每件商品涨价x元,则当售价为多少元时,该商品每天的销售利润最大,最大利润为多少元?
(3)为增加销售利润,营销部推出了以下两种销售方案:方案一:每件商品涨价不超过8元;方案二:每件商品的利润至少为24元,请比较哪种方案的销售利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c为正数,若关于x的一元二次方程ax2+bx+c=0有两个实数根,则关于x的方程a2x2+b2x+c2=0解的情况为( )
A.有两个不相等的正根B.有一个正根,一个负根
C.有两个不相等的负根D.不一定有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
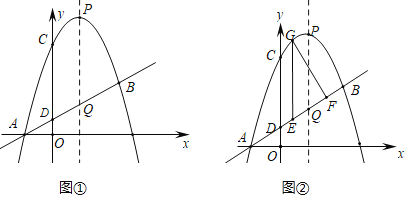
【题目】如图①抛物线y=﹣x2+(m﹣1)x+m与直线y=kx+k交于点A、B,其中A点在x轴上,它们与y轴交点分别为C和D,P为抛物线的顶点,且点P纵坐标为4,抛物线的对称轴交直线于点Q.
(1)试用含k的代数式表示点Q、点B的坐标.
(2)连接PC,若四边形CDQP的内部(包括边界和顶点)只有4个横坐标、纵坐标均为整数的点,求k的取值范围.
(3)如图②,四边形CDQP为平行四边形时,
①求k的值;
②E、F为线段DB上的点(含端点),横坐标分别为a,a+n(n为正整数),EG∥y轴交抛物线于点G.问是否存在正整数n,使满足tan∠EGF![]() 的点E有两个?若存在,求出n;若不存在说明理由.
的点E有两个?若存在,求出n;若不存在说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的![]() ,
,![]() ,
,![]() ,
,![]() 四个小区进行检査,并且每个小区不重复检查.
四个小区进行检査,并且每个小区不重复检查.
(1)甲组抽到![]() 小区的概率是___________;
小区的概率是___________;
(2)请用列表或画树状图的方法求甲组抽到![]() 小区,同时乙组抽到
小区,同时乙组抽到![]() 小区的概率.
小区的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一小球沿与地面成一定角度的方向飞出,小球的飞行路线是一条抛物线,如果不考虑空气阻力,小球的飞行高度h(单位:米)与飞行时间t(单位:秒)之间具有函数关系![]() ,请根据要求解答下列问题:
,请根据要求解答下列问题:

(1)在飞行过程中,当小球的飞行高度为15米时,需要多少飞行时间?
(2)在飞行过程中,小球飞行高度何时达到最大?最大高度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com