Question

【题目】在 Rt△ABC 中，∠BAC=90°，AC=AB，点 F 是射线 CA 上一点，连接 BF，过 C 作 CE⊥BF，垂足为点 E，直线 CE，AB 相交于点 D．

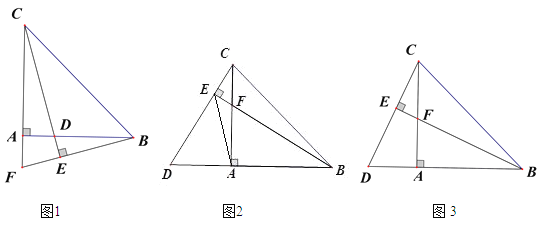
（1）如图 1，当点 F 在线段 CA 延长线上时，求证：AB+AD=CF；

（2）如图 2，当点 F 在线段 CA 上时，连接 EA，求证：EA 平分∠DEB；

（3）如图 3，当点 F 恰好为线段 CA 的中点时，EF=1，试求△BDE 的面积．

Answer 1

【答案】(1)证明见解析；(2) 证明见解析；(3)9

【解析】

（1）根据题意可以得到△ACD≌△ABF，然后根据全等三角形的性质可以证明结论成立．

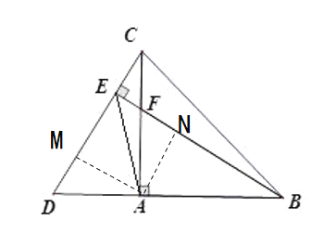
（2）过A作AM⊥CD于M, 作AN⊥BE于N可证Rt△CAM≌Rt△BAN，得到AM=AN，利用角平分线的判定即可证明；

(3)可证△CAD≌△BAF，设AD=AF=x则CF=AF=x, ，AB=AC=2x，由∠DCA=∠FCE，∠DAC=∠CEF=90°．可得 根据列出方程求出x的值，求出DE、BE的长即可得出答案．

(1)证明：∵∠BAC=90°，
∴∠CAD=∠FAB=90°．

∵CE⊥BF

∴∠DEB=90°．

∵∠ADC=∠EDB．

∴∠ACD=∠DBE

在Rt△CAD和Rt△BAF中，

，
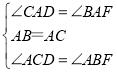∴Rt△CAD≌Rt△BAF，
∴AF=AD
∵AC+AF=CF

∴AB+AD=CF

(2)过A作AM⊥CD于M, 作AN⊥BE于N

∴∠CMA=∠BNA=90°．

∵∠BAC=90°，
∴∠CAD=∠FAB=90°．

∵CE⊥BF

∴∠BEC=90°．

∵∠CFE=∠AFB．

∴∠ACD=∠ABF

在Rt△CAM和Rt△BAN中，

，
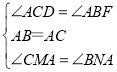∴Rt△CAM≌Rt△BAN

∴AM=AN

∵AM=AN, AM⊥CD, AN⊥BE

∴EA平分∠DEB

(3)∵CE⊥BF

∴∠BEC=90°．

∵∠CFE=∠AFB．

∴∠ACD=∠ABF

∵∠BAC=90°，
∴∠CAD=∠FAB=90°．

∵AC=AB

∴△CAD≌△BAF

∴AF=AD

设AD=AF=x

∵F为AC的中点

∴CF=AF=x,AC=2x

∴ ，AB=AC=2x

∵∠DCA=∠FCE，∠DAC=∠CEF=90°

∴

∴

∴

解得

∴

∴

∴DE=CD-CE=3

∴

∴