【方法介绍】
同学们，生活中的很多实际问题，我们往往抽象成数学问题，然后通过数形结合建立数学模型的方式来解决．
例如：学校举办足球赛，共有五个球队参加比赛，每个队都要和其他各队比赛一场，问该学校一共要安排多少场比赛？
这是一个实际问题，我们可以在平面内画出5个点（任意3个点都不在同一条直线上），如图①所示，其中每个点各代表一个足球队，两个队之间比赛一场就用一条线段把它们连起来，其中连接线段的条数就是安排比赛的场数．这样模型就建立起来了，如何解决这个模型呢？由于每个队都要与其他各队比赛一场，即每个点都要与另外4点连接一条线段，这样5个点应该有5×4=20条线段，而每两个点之间的线段都重复计算了一次，实际只有10条线段，所以学校一共要安排10场比赛．
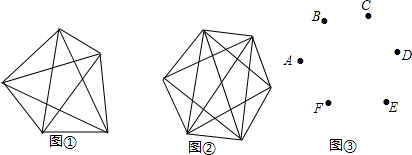
【学以致用】
（1）根据图②回答：如果有6个班级的足球队参加比赛，学校一共要安排
场比赛；
（2）根据规律，如果有n个班级的足球队参加比赛，学校一共要安排
场比赛．
【问题解决】
（1）小明今年参加了学校新组建的合唱队，老师让所有人每两人相互握手，认识彼此（每两人之间不重复握手）．小明发现所有人握手次数总和为91次，那么合唱队有多少人？
（2）A、B、C、D、E、F六人参加一次会议，见面时他们相互握手问好，每两人之间不重复握手，如图③，已知A已经握了5次，B已经握了4次，C已经握了3次，D已经握了2次，E已经握了1次，请利用图③分析F已经和哪些人握手了．
【问题拓展】
根据上述模型的建立和问题的解决，请你提出一个问题，并进行解答．
核心素养学练评系列答案
单元期中期末卷系列答案
