
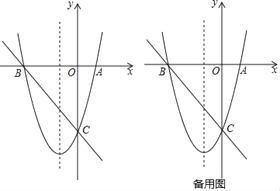
����Ŀ����ͼ����֪������y=![]() x2+3x��8��ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��
x2+3x��8��ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��
��1����ֱ��BC�Ľ���ʽ��
��2����F��ֱ��BC�·��������ϵ�һ�㣬����BCF��������ʱ���������ߵĶԳ�������һ��P��ʹ����BFP���ܳ���С���������F������͵�P�����ꣻ
��3���ڣ�2���������£��Ƿ���������ĵ�Q��0��m����ʹ����BFQΪ���������Σ�����У���ֱ��д����Q�����ꣻ���û�У���˵�����ɣ�
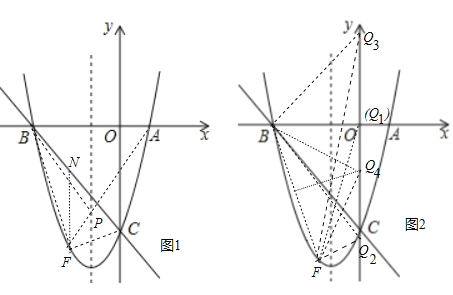
���𰸡���1��y=��x��8����2��F����4����12����P����3����10������3��������.
�������������������1�����ô���ϵ�������B��C�������꼴�ɽ��������
��2����ͼ1������FN��y�ύBC��N����F��m�� ![]() m2+3m��8������N��m����m��8�����������κ��������ö��κ��������������F��������Ϊ��B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С�����ֱ��AF�Ľ���ʽ���ɽ��������
m2+3m��8������N��m����m��8�����������κ��������ö��κ��������������F��������Ϊ��B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С�����ֱ��AF�Ľ���ʽ���ɽ��������
��3����ͼ2������������������������FQ1=FBʱ��Q1��0��0��������BF=BQʱ����֪Q2��0���� ![]() ����Q3��0��
����Q3��0�� ![]() ��������Q4B=Q4Fʱ����Q��0��m�����������̼��ɽ��������
��������Q4B=Q4Fʱ����Q��0��m�����������̼��ɽ��������
���������������1������������y=![]() x2+3x��8����y=0���õ���
x2+3x��8����y=0���õ��� ![]() x2+3x��8=0�������x=��8��2����B����8��0����A��2��0������x=0���õ���y=��8����A��2��0����B����8��0����C��0����8������ֱ��BC�Ľ���ʽΪy=kx+b��������
x2+3x��8=0�������x=��8��2����B����8��0����A��2��0������x=0���õ���y=��8����A��2��0����B����8��0����C��0����8������ֱ��BC�Ľ���ʽΪy=kx+b�������� ![]() �������
������� ![]() ����ֱ��BC�Ľ���ʽΪy=��x��8��
����ֱ��BC�Ľ���ʽΪy=��x��8��
��2����ͼ1������FN��y�ύBC��N����F��m�� ![]() m2+3m��8������N��m����m��8��
m2+3m��8������N��m����m��8��
��S��FBC=S��FNB+S��FNC=![]() FN��8=4FN=4[����m��8������
FN��8=4FN=4[����m��8������![]() m2+3m��8��]=��2m2��16m=��2��m+4��2+32������m=��4ʱ����FBC����������ֵ����ʱF����4����12�����������ߵĶԳ���x=��3��
m2+3m��8��]=��2m2��16m=��2��m+4��2+32������m=��4ʱ����FBC����������ֵ����ʱF����4����12�����������ߵĶԳ���x=��3��![]() �������
������� ![]() ����ֱ��AF�Ľ���ʽΪy=2x��4����P����3����10��������F������͵�P������ֱ���F����4����12����P����3����10����
����ֱ��AF�Ľ���ʽΪy=2x��4����P����3����10��������F������͵�P������ֱ���F����4����12����P����3����10����
��3����ͼ2�У���B����8��0����F����4��0������BF=![]() =
=![]() �����������������
�����������������
����FQ1=FBʱ��Q1��0��0����
����BF=BQʱ����֪Q2��0���� ![]() ����Q3��0��
����Q3��0�� ![]() ����
����
����Q4B=Q4Fʱ����Q4��0��m��������82+m2=42+��m+12��2�����m=��4����Q4��0����4��
��Q��������0��0����0�� ![]() ����0����
����0����![]() ����0����4����
����0����4����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
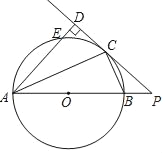
����Ŀ����ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬����C����O�����߽�AB���ӳ����ڵ�P������A��AD��PC�ڵ�D��AD���O���ڵ�E��
��1����֤��ACƽ�֡�DAB��
��2����AB��10��sin��CAB��![]() ����д����DE����˼·��
����д����DE����˼·��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
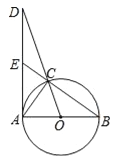
����Ŀ����ͼ����֪��O����ABΪֱ������ABC�����Բ������A����O�����߽�OC���ӳ����ڵ�D����BC���ӳ����ڵ�E��
��1����֤����DAC=��DCE��
��2����AB=2��sin��D=![]() ����AE�ij���
����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������OABC�ı�OC��OA�ֱ���x��y����������ϣ����B��4��4������P��t��0����x����һ���㣬����O��OH��AP�ڵ�H��ֱ��OH��ֱ��BC�ڵ�D����AD��
��1����ͼ1������P���߶�OC��ʱ����֤��OP��CD��
��2���ڵ�P�˶������У���AOP����A��B��DΪ���������������ʱ����t��ֵ��
��3����ͼ2��������y����![]() x2+
x2+![]() x+4���Ƿ���ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
x+4���Ƿ���ڵ�Q��ʹ����P��D��Q��CΪ������ı���Ϊƽ���ı��Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
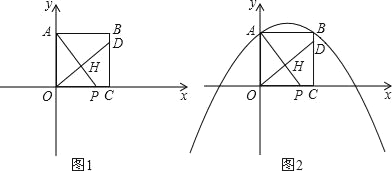
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1������ABC�У���BAC=90����AB=AC=2![]() ��D��E����ֱ���AC��BC�ϣ���DE��AB��DC=2
��D��E����ֱ���AC��BC�ϣ���DE��AB��DC=2![]() ������CDE�Ƶ�C˳ʱ����ת�õ���CD��E������ͼ2����D��E��Ӧ��ֱ�ΪD����E����D����E����AC�ཻ�ڵ�M����E���պ����ڱ�AB��ʱ����AMD�������Ϊ ��
������CDE�Ƶ�C˳ʱ����ת�õ���CD��E������ͼ2����D��E��Ӧ��ֱ�ΪD����E����D����E����AC�ཻ�ڵ�M����E���պ����ڱ�AB��ʱ����AMD�������Ϊ ��
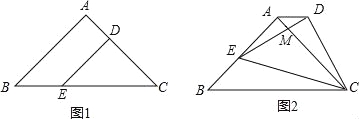
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��ABΪ10cm����BC=8cm����ACB��ƽ���߽���O�ڵ�D.����AD��BD.���ı���ABCD�����.
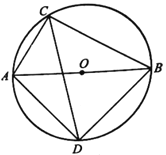
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�������������ξ�Ϊ200�ĺ���A�ͺ���B��һ����ɻ��ھ��뺣ƽ�洹ֱ�߶�Ϊ1100�Ŀ��з��У����е���C��ʱ�����ǰ��һ��������A�ĸ�����45����Ȼ����ƽ����AB�ķ���ˮƽ����1.99��104�����D������D�������ǰ����һ��������B�ĸ�����60��������������ľ���AB��
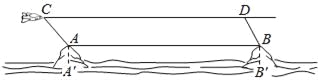
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
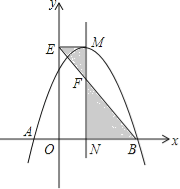
����Ŀ����ͼ��������![]() ��x�ύ��A��B���㣬���ǵĶԳ�����x�ύ�ڵ�N��������M��ME��y���ڵ�E������BE��MN�ڵ�F.��֪��A������Ϊ����1��0��.
��x�ύ��A��B���㣬���ǵĶԳ�����x�ύ�ڵ�N��������M��ME��y���ڵ�E������BE��MN�ڵ�F.��֪��A������Ϊ����1��0��.
��1����������ߵĽ���ʽ������M�����ꣻ
��2������EMF����BNF�����֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
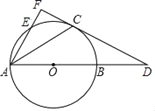
����Ŀ����ͼ��AB�ǡ�O��ֱ����CΪ��O��һ�㣬������C��ֱ����AB���ӳ��߽��ڵ�D������AC��BC����BCD����CAB��E�ǡ�O��һ�㣬��CB����CE������AE���ӳ���DC���ӳ��߽��ڵ�F��
��1����֤��DC�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ3��sin��D��![]() �����߶�AF�ij���
�����߶�AF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com