
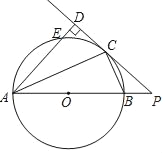
【题目】如图,AB是⊙O的直径,C为⊙O上一点,过点C作⊙O的切线交AB的延长线于点P,过点A作AD⊥PC于点D,AD与⊙O交于点E.
(1)求证:AC平分∠DAB.
(2)若AB=10,sin∠CAB=![]() ,请写出求DE长的思路.
,请写出求DE长的思路.
【答案】(1)证明见解析;(2)见解析
【解析】
(1)连接OC,PD切⊙O于点C,AD⊥PC于点D得到∠EAC=∠ACO,且OA=OC即可得到∠EAC=∠CAO得出结论.
(2)连接CE,由(1)中可得Rt△CDE∽Rt△ACB得出![]() ,即可求出BC,∠EAC=∠CAB根据圆的性质易得EC=BC=4,故得出DE=
,即可求出BC,∠EAC=∠CAB根据圆的性质易得EC=BC=4,故得出DE=![]() .
.
(1)证明:连接OC,
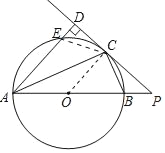
∵PD切⊙O于点C,
∴OC⊥PC,
∵AD⊥PC于点D,
∴OC∥AD,
∴∠EAC=∠ACO.
又∵OA=OC,
∴∠ACO=∠OAC,
∴∠EAC=∠CAO,
即AC平分∠DAB.
(2)解:连接CE,
可证:Rt△CDE∽Rt△ACB,
∴![]() ,
,
在Rt△ABC中,由AB=10,sin∠CAB=![]() ,
,
∴BC=4,
由∠EAC=∠CAB,得![]() ,
,
∴EC=BC=4.
故DE=![]() 可求.
可求.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
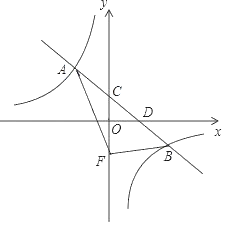
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
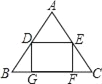
【题目】一块三角形材料如图所示,∠A=∠B=60°,用这块材料剪出一个矩形DEFG,其中,点D,E分别在边AB,AC上,点F,G在边BC上.设DE=x,矩形DEFG的面积s与x之间的函数解析式是s=﹣![]() x2+
x2+![]() x,则AC的长是_____.
x,则AC的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
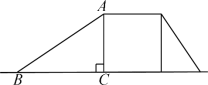
【题目】如图所示是某公园“六一”前新增设的一台滑梯.该滑梯的高度AC=2 m,滑梯着地点B与梯架之间的距离BC=4m.
(1)求滑梯AB的长(精确到0.1 m);
(2)若规定滑梯的倾斜角(∠ABC)不超过45°属于安全,请通过计算说明这架滑梯的倾斜角是否符合要求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
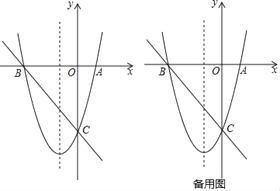
【题目】如图,已知抛物线y=![]() x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com