
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).

科目:初中数学 来源: 题型:
【题目】某批发市场批发甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润![]() (万元)与进货量
(万元)与进货量![]() (吨)近似满足函数关系
(吨)近似满足函数关系![]() ;乙种水果的销售利润
;乙种水果的销售利润![]() (万元)与进货量
(万元)与进货量![]() (吨)近似满足函数关系
(吨)近似满足函数关系![]() (其中
(其中![]() ,
,![]() ,
,![]() 为常数),且进货量
为常数),且进货量![]() 为
为![]() 吨时,销售利润
吨时,销售利润![]() 为
为![]() 万元;进货量
万元;进货量![]() 为
为![]() 吨时,销售利润
吨时,销售利润![]() 为
为![]() 万元.
万元.
![]() 求
求![]() (万元)与
(万元)与![]() (吨)之间的函数关系式.
(吨)之间的函数关系式.
![]() 如果市场准备进甲、乙两种水果共
如果市场准备进甲、乙两种水果共![]() 吨,设乙种水果的进货量为
吨,设乙种水果的进货量为![]() 吨,请你写出这两种水果所获得的销售利润之和
吨,请你写出这两种水果所获得的销售利润之和![]() (万元)与
(万元)与![]() (吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润之和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某渔业养殖场,对每天打捞上来的鱼,一部分由工人运到集贸市场按10元/斤销售,剩下的全部按3元/斤的购销合同直接包销给外面的某公司:养殖场共有30名工人,每名工人只能参与打捞与到集贸市场销售中的一项工作,且每人每天可以打捞鱼100斤或销售鱼50斤,设安排x名员工负责打捞,剩下的负责到市场销售.
(1)若养殖场一天的总销售收入为y元,求y与x的函数关系式;
(2)若合同要求每天销售给外面某公司的鱼至少200斤,在遵守合同的前提下,问如何分配工人,才能使一天的销售收入最大?并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,2),点B为一、三象限角平分线上的一个动点,BC⊥AB交x轴的正半轴于点C.当∠OAB=_____°时,△COB是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O.
(1)画出△AOB平移后的三角形,其平移后的方向为射线AD的方向,平移的距离为AD的长.
(2)观察平移后的图形,除了矩形ABCD外,还有一种特殊的平行四边形?请证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
与x轴交于A,B两点(点A在点B的左边),与y轴正半轴交于点C.
(1)如图1,若A(-1,0),B(3,0),
① 求抛物线![]() 的解析式;
的解析式;
② P为抛物线上一点,连接AC,PC,若∠PCO=3∠ACO,求点P的横坐标;
(2)如图2,D为x轴下方抛物线上一点,连DA,DB,若∠BDA+2∠BAD=90°,求点D的纵坐标.

![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+2x+2m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若x1,x2是一元二次方程x2+2x+2m=0的两个根,且x12+x22﹣x1x2=8,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 的面积为6.
的面积为6.

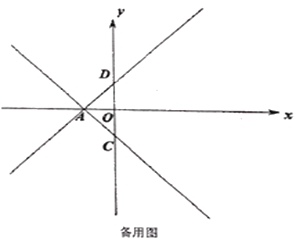
(1)求![]() 和
和![]() 的值.
的值.
(2)如图1,将直线![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 得到直线
得到直线![]() ,点
,点![]() 在
在![]() 轴上,若点
轴上,若点![]() 为
为![]() 轴上的一个动点,点
轴上的一个动点,点![]() 为直线
为直线![]() 上的一个动点,当
上的一个动点,当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标及
的坐标及![]() 的最小值.
的最小值.
(3)如图2,将![]() 沿着直线
沿着直线![]() 平移得到
平移得到![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 是等腰三角形时,求此时
是等腰三角形时,求此时![]() 点坐标.
点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com