
【题目】如图1,已知直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 的面积为6.
的面积为6.

(1)求![]() 和
和![]() 的值.
的值.
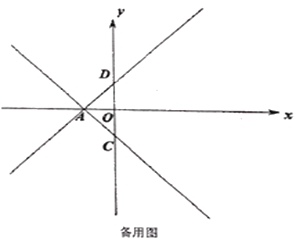
(2)如图1,将直线![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 得到直线
得到直线![]() ,点
,点![]() 在
在![]() 轴上,若点
轴上,若点![]() 为
为![]() 轴上的一个动点,点
轴上的一个动点,点![]() 为直线
为直线![]() 上的一个动点,当
上的一个动点,当![]() 的值最小时,求此时点
的值最小时,求此时点![]() 的坐标及
的坐标及![]() 的最小值.
的最小值.
(3)如图2,将![]() 沿着直线
沿着直线![]() 平移得到
平移得到![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 是等腰三角形时,求此时
是等腰三角形时,求此时![]() 点坐标.
点坐标.
【答案】(1)![]() ,b=-2,;(2)M(
,b=-2,;(2)M(![]() ,0),
,0),![]() 的最小值为
的最小值为![]() ;(3)当
;(3)当![]() 是等腰三角形时,P(2,0)或P(6,0).
是等腰三角形时,P(2,0)或P(6,0).
【解析】
(1)根据![]() 得到点C的坐标,代入
得到点C的坐标,代入![]() 得到b=-2,根据
得到b=-2,根据![]() 的面积为6,求出点B的坐标,代入
的面积为6,求出点B的坐标,代入![]() 即可求出k的值;
即可求出k的值;
(2)根据点A、C的坐标求出∠OAC=45![]() ,由将直线
,由将直线![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 得到直线
得到直线![]() ,点
,点![]() 在
在![]() 轴上,得到OD=OA=2,过点A作A
轴上,得到OD=OA=2,过点A作A![]() ⊥x轴,且A
⊥x轴,且A![]() =AB=6-(-2)=8,连接B
=AB=6-(-2)=8,连接B![]() ,此时点B与点
,此时点B与点![]() 关于直线AD对称,连接
关于直线AD对称,连接![]() C交直线AD于点N,交x轴于点M,此时
C交直线AD于点N,交x轴于点M,此时![]() 的值最小,利用勾股定理求出
的值最小,利用勾股定理求出![]() C的长度即可;
C的长度即可;
(3)根据平移设点![]() 的坐标为(c,-c-2),由平移设直线
的坐标为(c,-c-2),由平移设直线![]() 的解析式为y=x+m,利用点
的解析式为y=x+m,利用点![]() 求得直线
求得直线![]() 的解析式为y=x-2c-2,得到点P(2c+2,0),利用勾股定理求得
的解析式为y=x-2c-2,得到点P(2c+2,0),利用勾股定理求得![]() 、
、![]() 、
、![]() ,分三种情况求出c的值,即可得到点P的坐标.
,分三种情况求出c的值,即可得到点P的坐标.
(1)令![]() 中x=0,得y=-2,∴C(0,-2),∴OC=2,
中x=0,得y=-2,∴C(0,-2),∴OC=2,
将点C的坐标代入![]() 中,得b=-2,
中,得b=-2,
∴直线AC的解析式为y=-x-2,
∵![]() 的面积为6,
的面积为6,
∴![]() ,
,
∴OB=6,点B的坐标为(6,0),
将点B的坐标代入![]() 中,得6k-2=0,∴
中,得6k-2=0,∴![]() ;
;
(2)
∵直线AC的解析式为y=-x-2,
∴当y=0时,x=-2,∴A(-2,0),
∴OA=OC,
∴∠OAC=45![]() ,
,
∵将直线![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 得到直线
得到直线![]() ,点
,点![]() 在
在![]() 轴上,
轴上,
∴∠OAD=45![]() ,
,
∴OD=OA=2,
过点A作A![]() ⊥x轴,且A
⊥x轴,且A![]() =AB=6-(-2)=8,连接B
=AB=6-(-2)=8,连接B![]() ,此时点B与点
,此时点B与点![]() 关于直线AD对称,连接
关于直线AD对称,连接![]() C交直线AD于点N,交x轴于点M,此时
C交直线AD于点N,交x轴于点M,此时![]() 的值最小.
的值最小.
设直线![]() 的解析式为y=dx+e,将点C(0,-2),
的解析式为y=dx+e,将点C(0,-2), ![]() (-2,8)代入,得
(-2,8)代入,得
![]() ,得
,得![]() ,∴直线
,∴直线![]() 的解析式为y=-5x-2,
的解析式为y=-5x-2,
当y=0时,![]() ,∴M(
,∴M(![]() ,0),
,0),
∵OC=OA=OD,
∴DM=MC,
∵BN=![]() N,
N,
∴![]()
=MC+MN+![]() N,
N,
=![]() C,
C,
过点C作CE⊥A![]() ,
,
∴CE=2,![]() E=10,
E=10,
∴![]() C=
C=![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.

(3)设直线AD的解析式为y=ax+n,将点A(-2,0),D(0,2)代入,
∴![]() ,得
,得![]()
∴设直线AD的解析式为y=x+2,
由(2)知:直线AC的解析式为y=-x-2,
设点![]() 的坐标为(c,-c-2),
的坐标为(c,-c-2),
由平移设直线![]() 的解析式为y=x+m,将点
的解析式为y=x+m,将点![]() 的坐标代入,得
的坐标代入,得
c+m=-c-2,
m=-2c-2,
∴直线![]() 的解析式为y=x-2c-2,
的解析式为y=x-2c-2,
当y=0时,x=2c+2,∴P(2c+2,0),
过点![]() 作
作![]() H⊥x轴于H,作
H⊥x轴于H,作![]() E⊥y轴于E,
E⊥y轴于E,
∴![]() =2c+2-c=c+2,
=2c+2-c=c+2, ![]() =c+2,
=c+2,![]() E=c,DE=2-(-c-2)=c+4,
E=c,DE=2-(-c-2)=c+4,
∴![]() ,
,
![]() ,
,
![]() ,
,
当![]() 是等腰三角形时,分三种情况:
是等腰三角形时,分三种情况:
①当![]() P=
P=![]() D时,得
D时,得![]() ,方程无解,舍去;
,方程无解,舍去;
②当![]() P=PD时,得
P=PD时,得![]() ,得c=0,
,得c=0,
∴P(2,0),
③当![]() D=PD时,得
D=PD时,得![]() ,得c=2或,c=-2(舍去),
,得c=2或,c=-2(舍去),
∴P(6,0),
综上,当![]() 是等腰三角形时,P(2,0)或P(6,0).
是等腰三角形时,P(2,0)或P(6,0).


科目:初中数学 来源: 题型:
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.
求证:
(1)CD⊥DF;
(2)BC=2CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“唯有书香气,引得大咖来”. 2019年2月14日至15日,由北京师范大学国际写作中心、重庆市第一中学校共同发起的主题为“阅读与写作”——首届“作家进校园”与“校园写作计划”活动隆重举行. 10余位国内文学大咖云集一中校园,开启大师课堂,页再次在校园掀起了读书热潮. 学校图书馆准备购进甲、乙两种书籍若干册供师生阅读,已知购买3册甲种书和4册乙种书共需265元;购买8册甲种书和7册乙种书共需560元.
(1)求甲种、乙种书籍每册各多少元?
(2)学校图书馆计划采购甲、乙两种书籍共710册,沙坪坝新华书店对重庆一中图书馆给予优惠,甲种书的单价不变,而乙种书的单价降价10%,这样购买乙种书的总价仍不低于甲种书的总价,则校图书馆至少需要投入多少资金才能完成采购计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学上,我们把符合一定条件的动点所形成的图形叫做满足该条件的点的轨迹.例如:动点P的坐标满足(m,m﹣1),所有符合该条件的点组成的图象在平面直角坐标系xOy中就是一次函数y=x﹣1的图象.即点P的轨迹就是直线y=x﹣1.
(1)若m、n满足等式mn﹣m=6,则(m,n﹣1)在平面直角坐标系xOy中的轨迹是 ;
(2)若点P(x,y)到点A(0,1)的距离与到直线y=﹣1的距离相等,求点P的轨迹;
(3)若抛物线y=![]() 上有两动点M、N满足MN=a(a为常数,且a≥4),设线段MN的中点为Q,求点Q到x轴的最短距离.
上有两动点M、N满足MN=a(a为常数,且a≥4),设线段MN的中点为Q,求点Q到x轴的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为点P,过B点的直线与线段AD的延长线交于点F,且∠F=∠ABC.
(1)如图1,求证:直线BF是⊙O的切线;
(2)如图2,当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过C作AE的垂线CF,垂足为F,过B作BD⊥BC交CF的延长线于点D

(1)试说明:AE=CD;
(2)AC=12cm,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com