【题目】李明到离家2.1千米的学校参加初三联欢会，到学校时发现演出道具还放在家中，此时距联欢会开始还有42分钟，于是他立即匀速步行回家，在家拿道具用了1分钟，然后立即匀速骑自行车返回学校．已知李明骑自行车到学校比他从学校步行到家用时少20分钟，且骑自行车的速度是步行速度的3倍．
(1)李明步行的速度(单位：米/分)是多少？
(2)李明能否在联欢会开始前赶到学校？
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，l1、l2、l3两两相交于A、B、C三点，它们与y轴正半轴分别交于点D、E、F，若A、B、C三点的横坐标分别为1、2、3，且OD=DE=1，则下列结论正确的个数是（ ）
①
，②S△ABC=1，③OF=5，④点B的坐标为（2，2.5）
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线
与x轴交于A，B两点（点A在点B的左边），与y轴正半轴交于点C.
（1）如图1，若A（－1，0），B（3，0），
① 求抛物线的解析式；
② P为抛物线上一点，连接AC，PC，若∠PCO=3∠ACO，求点P的横坐标；
（2）如图2，D为x轴下方抛物线上一点，连DA，DB，若∠BDA+2∠BAD=90°，求点D的纵坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，直线
与
轴、
轴分别交于点
、点
，直线
与轴、轴分别交于分别交于点
、点
，直线的解析式为
，直线的解析式为
，两直线交于点
，且
.
(1)求直线的解析式；
(2)将直线向下平移一定的距离，使得平移后的直线经过点，且与轴交于点
，求四边形
的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
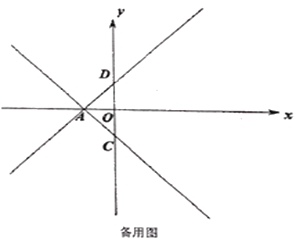
【题目】如图1，已知直线
的解析式为
，直线
的解析式为
，且
的面积为6.
(1)求
和
的值.
(2)如图1，将直线绕
点逆时针旋转
得到直线
，点
在
轴上，若点
为
轴上的一个动点，点
为直线上的一个动点，当
的值最小时，求此时点的坐标及的最小值.
(3)如图2，将
沿着直线平移得到
，
与轴交于点
，连接
、
，当
是等腰三角形时，求此时点坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，将绕点
旋转角
得
，
交
于点
，
分别交、
于
、
两点．
在旋转过程中，线段
与
有怎样的数量关系？证明你的结论；
当
时，试判断四边形
的形状，并说明理由；
在的情况下，求线段
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】自学下面材料后，解答问题．
分母中含有未知数的不等式叫分式不等式．如：
;
＜0等．那么如何求出它们的解集呢？
根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负．其字母表达式为：
（1）若a＞0，b＞0，则
＞0；若a＜0，b＜0，则＞0；
（2）若a＞0，b＜0，则＜0；若a＜0，b＞0，则＜0．
反之：（1）若＞0，则
或
（2）若＜0，则 或 ．
根据上述规律，求不等式
＞0的解集．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
