
【题目】在![]() 中,
中,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 旋转角
旋转角![]() 得
得![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 分别交
分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点.
两点.
![]() 在旋转过程中,线段
在旋转过程中,线段![]() 与
与![]() 有怎样的数量关系?证明你的结论;
有怎样的数量关系?证明你的结论;
![]() 当
当![]() 时,试判断四边形
时,试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 在
在![]() 的情况下,求线段
的情况下,求线段![]() 的长.
的长.

【答案】(1)![]() .理由见解析;
.理由见解析;![]() 四边形
四边形![]() 是菱形.理由见解析;
是菱形.理由见解析;![]() .
.
【解析】
(1)根据等边对等角的性质可得∠A=∠C,再根据旋转的性质可得∠ABE=∠C1BF,AB=BC=A1B=BC1,然后利用“角边角”证明△ABE和△C1BF全等,根据全等三角形对应边相等可得BE=BF,从而得解;
(2)先根据旋转的性质求出∠ABC1=150°,再根据同旁内角互补,两直线平行求出AB∥C1D,AD∥BC1,证明四边形BC1DA是平行四边形,又因为邻边相等,所以四边形BC1DA是菱形;
(3)过点E作EG⊥AB于点G,等腰三角形三线合一的性质可得AG=BG=2,然后解直角三角形求出AE的长度,再利用DE=AD-AE计算即可得解.
(1)![]() .理由如下:
.理由如下:
∵![]() ,
,
∴![]() ,
,
∵![]() 绕点
绕点![]() 顺时针旋转角
顺时针旋转角![]() 得
得![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
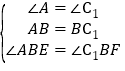 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
![]() 四边形
四边形![]() 是菱形.理由如下:
是菱形.理由如下:
∵旋转角![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
又∵![]() ,
,
∴四边形![]() 是菱形;
是菱形;
![]() 过点
过点![]() 作
作![]() ,
,

∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
由![]() 知
知![]() ,
,
∴![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为( )

A. 8![]() B. 8 C. 4
B. 8 C. 4![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,点P是直径AB上任意一点,过点P作弦CD⊥AB,垂足为点P,过B点的直线与线段AD的延长线交于点F,且∠F=∠ABC.
(1)如图1,求证:直线BF是⊙O的切线;
(2)如图2,当点P与点O重合时,过点A作⊙O的切线交线段BC的延长线于点E,在其它条件不变的情况下,判断四边形AEBF是什么特殊的四边形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标平面内,△ABC的三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).

(1)填空:∠ ABC= ,S△ABC= ;
(2)画出△ABC关于x轴的对称图形△A1B1C1,再画出△A1B1C1关于y轴的对称图形△A2B2C2,在x轴上作一点p,使p到A,C两点间的距离和最短;
(3)若M是△ABC内一点,其坐标是(a,b),则△A2B2C2中,点M的对应点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=90°,AB=2AC,点A(2,0)、B(0,4),点C在第一象限内,双曲线y=![]() (x>0)经过点C.将△ABC沿y轴向上平移m个单位长度,使点A恰好落在双曲线上,则m的值为________.
(x>0)经过点C.将△ABC沿y轴向上平移m个单位长度,使点A恰好落在双曲线上,则m的值为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A. 中位数是50 B. 众数是51 C. 方差是42 D. 极差是21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象经过点A(﹣3,﹣2).
的图象经过点A(﹣3,﹣2).
(1)求反比例函数的解析式;
(2)若点B(1,m),C(3,n)在该函数的图象上,试比较m与n的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com