Question

【题目】抛物线与x轴交于A，B两点（点A在点B的左边），与y轴正半轴交于点C.

（1）如图1，若A（－1，0），B（3，0），

① 求抛物线的解析式；

② P为抛物线上一点，连接AC，PC，若∠PCO=3∠ACO，求点P的横坐标；

（2）如图2，D为x轴下方抛物线上一点，连DA，DB，若∠BDA+2∠BAD=90°，求点D的纵坐标.

Answer 1

【答案】（1）①y=-x2+2x+3②（2）-1

【解析】（1）①把A、B的坐标代入解析式，解方程组即可得到结论；

②延长CP交x轴于点E，在x轴上取点D使CD=CA，作EN⊥CD交CD的延长线于N．由CD=CA ，OC⊥AD，得到∠DCO=∠ACO．由∠PCO=3∠ACO，得到∠ACD=∠ECD，从而有tan∠ACD=tan∠ECD，

，即可得出AI、CI的长，进而得到．设EN=3x，则CN=4x，由tan∠CDO=tan∠EDN，得到，故设DN=x，则CD=CN-DN=3x=，解方程即可得出E的坐标，进而求出CE的直线解析式，联立解方程组即可得到结论；

（2）作DI⊥x轴，垂足为I．可以证明△EBD∽△DBC，由相似三角形对应边成比例得到，

即，整理得．令y=0，得：．

故，从而得到．由，得到，解方程即可得到结论．

（1）①把A（－1，0），B（3，0）代入得：

，解得：，

∴

②延长CP交x轴于点E，在x轴上取点D使CD=CA，作EN⊥CD交CD的延长线于N．

∵CD=CA ，OC⊥AD，∴ ∠DCO=∠ACO．

∵∠PCO=3∠ACO，∴∠ACD=∠ECD，∴tan∠ACD=tan∠ECD，

∴，AI=，

∴CI=，∴．

设EN=3x，则CN=4x．

∵tan∠CDO=tan∠EDN，

∴，∴DN=x，∴CD=CN-DN=3x=，

∴，∴DE= ，E(，0)．

CE的直线解析式为：，

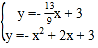
，解得：．

点P的横坐标 ．

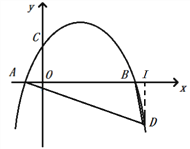
（2）作DI⊥x轴，垂足为I．

∵∠BDA+2∠BAD=90°，∴∠DBI+∠BAD=90°．

∵∠BDI+∠DBI=90°，∴∠BAD=∠BDI．

∵∠BID=∠DIA，∴△EBD∽△DBC，∴，

∴，

∴．

令y=0，得：．

∴，∴．

∵，

∴，

解得：yD=0或－1．

∵D为x轴下方一点，

∴，

∴D的纵坐标－1 ．