Question

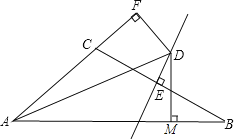
【题目】如图，在中，的平分线和边的垂直平分线相交于点，过点作垂直于交的延长线于点，若，则的长为__________．

Answer 1

【答案】

【解析】

根据角平分线的性质结合全等三角形的判定定理得出△AFD≌△AMD，即可得出AF=AM，再利用线段垂直平分线的性质得出CD=BD，根据HL得出Rt△CDF≌Rt△BDM，即可得出CF=BM，即可得出答案．

如图，连接CD，DB，作DM⊥AB于一点M，

∵AD平分∠A，
∴，

在△AFD和△AMD中，，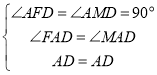
∴△AFD≌△AMD(AAS)，
∴AF=AM，
∵DE垂直平分线BC，
∴CD=BD（线段垂直平分线上的点到线段两端点距离相等），

∵AD平分∠A，DF⊥AC，DM⊥AB，
∴DF=DM（角平分线上的点到角的两边距离相等）
∵∠AFD=∠DMB=90°，

∴Rt△CDF≌Rt△BDM(HL)，
∴BM=CF，

∵，

，

又∵，

∴，

∴，

故答案为：．