
【题目】如图,⊙O的直径AB为10cm,弦BC=8cm,∠ACB的平分线交⊙O于点D.连接AD,BD.求四边形ABCD的面积.
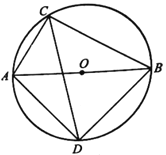
【答案】S四边形ADBC=49(cm2).
【解析】
根据直径所对的角是90°,判断出△ABC和△ABD是直角三角形,根据圆周角∠ACB的平分线交⊙O于D,判断出△ADB为等腰直角三角形,根据勾股定理求出AD、BD、AC的值,再根据S四边形ADBC=S△ABD+S△ABC进行计算即可.
∵AB为直径,
∴∠ADB=90°,
又∵CD平分∠ACB,即∠ACD=∠BCD,
∴![]() ,
,
∴AD=BD,
∵直角△ABD中,AD=BD,AD2+BD2=AB2=102,
则AD=BD=5![]() ,
,
则S△ABD=![]() ADBD=
ADBD=![]() ×5
×5![]() ×5
×5![]() =25(cm2),
=25(cm2),
在直角△ABC中,AC=![]() =6(cm),
=6(cm),
则S△ABC=![]() ACBC=
ACBC=![]() ×6×8=24(cm2),
×6×8=24(cm2),
则S四边形ADBC=S△ABD+S△ABC=25+24=49(cm2).


科目:初中数学 来源: 题型:
【题目】为了保证端午龙舟赛在我市汉江水域顺利举办,某部门工作人员乘快艇到汉江水域考察水情,以每秒10米的速度沿平行于岸边的赛道AB由西向东行驶.在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
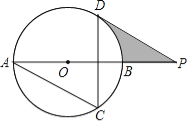
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
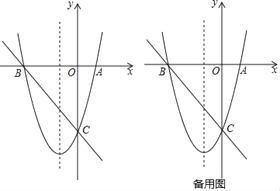
【题目】如图,已知抛物线y=![]() x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
x2+3x﹣8的图象与x轴交于A,B两点(点A在点B的右侧),与y轴交于点C.
(1)求直线BC的解析式;
(2)点F是直线BC下方抛物线上的一点,当△BCF的面积最大时,在抛物线的对称轴上找一点P,使得△BFP的周长最小,请求出点F的坐标和点P的坐标;
(3)在(2)的条件下,是否存在这样的点Q(0,m),使得△BFQ为等腰三角形?如果有,请直接写出点Q的坐标;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学用圆规BOA画一个半径为4cm的圆,测得此时∠O=90°,为了画一个半径更大的同心圆,固定A端不动,将B端向左移至B′处,此时测得∠O′=120°,则BB′的长为_______厘米

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中,AB=6cm,BC=8cm,动点 P 以 2cm/s 的速度从点 A 出发,沿AC 向点 C 移动,同时动点 Q 以 1cm/s 的速度从点 C 出发,沿 CB 向点 B 移动,设 P、Q 两点移动 ts(0<t<5)后,△CQP 的面积为 Scm2.在 P、Q 两点移动的过程中,△CQP 的面积能否等于 3.6cm2?若能,求出此时 t 的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
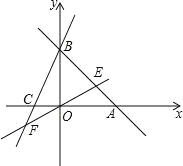
【题目】直线AB:y=﹣x+b分别与x,y轴交于A(6,0)、B 两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标.
(2)求直线BC的解析式.
(3)直线 EF 的解析式为y=x,直线EF交AB于点E,交BC于点 F,求证:S△EBO=S△FBO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com