练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．计算：（$\frac{1}{2}$b2-4a2）•（-4ab）=-2ab3+16a3b．

    分析 直接利用单项式乘以多项式运算法则求出即可．

    解答 解：（$\frac{1}{2}$b2-4a2）•（-4ab）=-2ab3+16a3b．
    故答案为：-2ab3+16a3b．

    点评 此题主要考查了单项式乘以多项式，正确掌握运算法则是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    18．下列句子不是真命题的是（　　）
    A．两直线平行，同位角相等B．同旁内角互补，两直线平行
    C．若a2=b2，则a=bD．对顶角相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

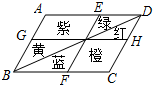    19．闵行体育公园内有一个形状是平行四边形的花坛（如图），并且AB∥EF∥DC，BC∥GH∥AD，花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花．如果小杰不小心把球掉入花坛，那么下列说法中错误的是（　　）
    A．球落在红花丛中和绿花丛中的概率相等
    B．球落在紫花丛中和橙花丛中的概率相等
    C．球落在红花丛中和蓝花丛中的概率相等
    D．球落在蓝花丛中和黄花丛中的概率相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．不等式组$\left\{\begin{array}{l}x+1＞0\\ 2x-2≤0\end{array}$的解集在数轴上表示为（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图1，四边形ABCD中，AB=BC，BE⊥AD，垂足为E，∠BCD-ABE=90°，过点C作CF∥AD，交对角线BD于点F．
    （1）求证：CF=CD；
    （2）若将“AB=BC”改为“AB=k•BC（k为常数，且k＞0）”，其它条件不变（如图2），求$\frac{CF}{CD}$的值（用含k的式子表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．先化简，再求值：（x+2）（x-2）-5x（x-1）-（2x+1）2，其中x=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，在平面直角坐标系中，正方形ABCD的边长为1，AD边的中点处有一动点P，动点P沿P→A→B→C→D→P运动一周，则点P的纵坐标y与点P走过的路程x之间的函数关系用图象表示大致是（　　）
    A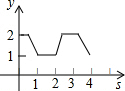．B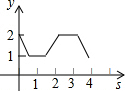．C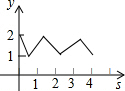．D．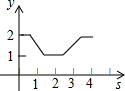

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．m2-m+$\frac{1}{4}$=（m-$\frac{1}{2}$）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

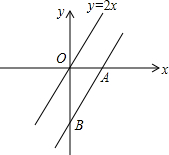    18．如图，把直线y=2x向下平移后得到直线AB，直线AB与x轴、y轴分别相交于点A、B．若△ABO的面积是1，则直线AB的解析式是（　　）
    A．y=3x+$\sqrt{2}$B．y=2x-$\sqrt{2}$C．y=3x-2D．y=2x-2

    查看答案和解析>>

    同步练习册答案