
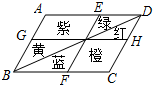
 闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )
闵行体育公园内有一个形状是平行四边形的花坛(如图),并且AB∥EF∥DC,BC∥GH∥AD,花坛中分别种有红、黄、蓝、绿、橙、紫6种颜色的花.如果小杰不小心把球掉入花坛,那么下列说法中错误的是( )| A. | 球落在红花丛中和绿花丛中的概率相等 | |
| B. | 球落在紫花丛中和橙花丛中的概率相等 | |
| C. | 球落在红花丛中和蓝花丛中的概率相等 | |
| D. | 球落在蓝花丛中和黄花丛中的概率相等 |
分析 根据平行四边形的性质可知GH、BD、EF把一个平行四边形分割成四个小平行四边形,我们知道,一条对角线可以把一个平行四边形的面积一分为二,据此可从图中获得S黄=S蓝,S绿=S红,S(紫+黄+绿)=S(橙+红+蓝),根据等量相减原理知S紫=S橙,依此就可找出题中说法错误的.
解答 解:∵AB∥EF∥DC,BC∥GH∥AD
∴GH、BD、EF把一个平行四边形分割成四个小平行四边形,
∴一条对角线可以把一个平行四边形的面积一分为二,
得S黄=S蓝,S绿=S红
∴球落在蓝花丛中和黄花丛中的概率相等(故D正确);球落在红花丛中和绿花丛中的概率相等(故A正确);
S(紫+黄+绿)=S(橙+红+蓝),
根据等量相减原理知S紫=S橙,
∴球落在紫花丛中和橙花丛中的概率相等(故B正确);
S红与S蓝显然不相等
∴球落在红花丛中和蓝花丛中的概率不相等(故C错误).
故选:C.
点评 本题考查的是平行四边形的性质及几何概率的知识,平行四边形的一条对角线可以把平行四边形分成两个全等的三角形,两条对角线把平行四边形的面积一分为四,同时充分利用等量相加减原理解题,否则容易从直观上对S红等于S蓝产生质疑.


科目:初中数学 来源: 题型:解答题
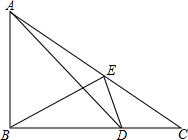 如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.
如图,△ABC中,∠ABC=90°,D为BC上一点,且BD=AB,连接AD,E是AC上一点,∠ABE=∠BDE且∠C+2∠EBC=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x}^{2}+1}=0$ | B. | $\sqrt{x-2}+\frac{1}{2}=0$ | C. | $\sqrt{x+1}=2$ | D. | $\sqrt{x-1}+\sqrt{1-x}=2$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
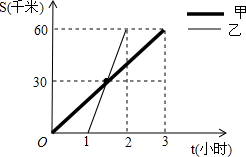 甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:
甲、乙两车分别从A地将一批物资运往B地,两车离A地的距离s(千米)与其相关的时间t(小时)变化的图象如图所示.读图后填空:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com