
°æƒø°ø‘ƒ∂¡≤ƒ¡œ£∫æðÀµ£¨Œ“π˙÷¯√˚ ˝—ߺ“ª™¬Þ∏˝‘⁄≥ˆπ˙∑√Œ Õæ÷–£¨ø¥µΩ∑…ª˙…œ¡⁄◊˘µƒ≥ÀøÕ‘ƒ∂¡µƒ‘”÷æ…œ”–“ªµ¿÷«¡¶Ã‚£∫“ª∏ˆ ˝ «59319£¨œ£Õ˚«ÛÀ¸µƒ¡¢∑Ω∏˘.ª™¬Þ∏˝Õ—ø⁄∂¯≥ˆ£∫39£¨¡⁄◊˘µƒ≥ÀøÕ Æ∑÷æ™∆Ê£¨√¶Œ º∆À„µƒ∞¬√Ó.
ƒ„÷™µ¿ª™¬Þ∏˝ «‘ı—˘—∏ÀŸ◊º»∑µÿº∆À„≥ˆ¿¥µƒ¬£øÀ˚ «∞¥’’œ¬√ʵƒ∑Ω∑®»∑∂®µƒ:
”…![]() £¨
£¨![]() £¨æՃл∑∂®
£¨æՃл∑∂®![]() «2Œª ˝.”…59319µƒ∏ˆŒª…œµƒ ˝ «9£¨æՃл∑∂®
«2Œª ˝.”…59319µƒ∏ˆŒª…œµƒ ˝ «9£¨æՃл∑∂®![]() µƒ∏ˆŒª…œµƒ ˝ «9£¨»Áπ˚ªÆ»•59319∫Û√ʵƒ»˝Œª319µ√µΩ ˝59£¨∂¯
µƒ∏ˆŒª…œµƒ ˝ «9£¨»Áπ˚ªÆ»•59319∫Û√ʵƒ»˝Œª319µ√µΩ ˝59£¨∂¯![]() £¨
£¨![]() £¨”…¥Àø…»∑∂®
£¨”…¥Àø…»∑∂®![]() µƒ ÆŒª…œµƒ ˝ «3£¨À˘“‘£¨
µƒ ÆŒª…œµƒ ˝ «3£¨À˘“‘£¨![]() .
.
£®1£©“—÷™19683£¨110592∂º «’˚ ˝µƒ¡¢∑Ω£¨∞¥’’…œ ˆ∑Ω∑®£¨«Î÷±Ω”–¥≥ˆÀ¸√«µƒ¡¢∑Ω∏˘£ª
£®2£©![]() «Œ“√«√ª”–—ßœ∞π˝µƒÀƒ¥Œ∑Ω∏˘£¨«“À¸µƒΩ·π˚“≤ «“ª∏ˆ’˚ ˝£¨«Îƒ„∏˘æð≤ƒ¡œµƒ∑Ω∑®«Û≥ˆΩ·π˚£¨≤¢Àµ√˜¿Ì”….
«Œ“√«√ª”–—ßœ∞π˝µƒÀƒ¥Œ∑Ω∏˘£¨«“À¸µƒΩ·π˚“≤ «“ª∏ˆ’˚ ˝£¨«Îƒ„∏˘æð≤ƒ¡œµƒ∑Ω∑®«Û≥ˆΩ·π˚£¨≤¢Àµ√˜¿Ì”….
°æ¥∞∏°ø£®1£©![]() £¨
£¨![]() £ª£®2£©
£ª£®2£©![]() .
.
°æΩ‚Œˆ°ø
£®1£©∑÷±∏˘æðÂ÷–À˘∏¯µƒ∑÷Œˆ∑Ω∑®œ»«Û≥ˆ’‚¡Ω∏ˆ ˝µƒ¡¢∑Ω∏˘∂º «¡ΩŒª ˝£¨»ª∫Û‘Ÿ«Û≥ˆ∏ˆŒª ˝∫Õ ÆŒª ˝º¥ø…£ª
£®2£©∑÷±∏˘æðÂ÷–À˘∏¯µƒ∑÷Œˆ∑Ω∑®œ»«Û≥ˆ’‚∏ˆ ˝µƒÀƒ¥Œ∑Ω∏˘ «¡ΩŒª ˝£¨»ª∫Û‘Ÿ«Û≥ˆ∏ˆŒª ˝∫Õ ÆŒª ˝º¥ø…£¨—È÷§∫Ûø…µ√Ω·π˚.
Ω‚£∫£®1£©”…“‚µ√£∫Â÷–À˘∏¯≥ˆ ˝µƒ¡¢∑Ω∏˘∂º «¡ΩŒª ˝£¨
°þ19683µƒ∏ˆŒª…œµƒ ˝ «3£¨æՃл∑∂®![]() µƒ∏ˆŒª…œµƒ ˝ «7£¨19683»•µÙ∫Û3Œªµ√µΩ19£¨
µƒ∏ˆŒª…œµƒ ˝ «7£¨19683»•µÙ∫Û3Œªµ√µΩ19£¨
°þ23£º19£º33£¨
°ý![]() µƒ ÆŒª…œµƒ ˝ «2£¨
µƒ ÆŒª…œµƒ ˝ «2£¨
°ý![]() £ª
£ª
°þ110592µƒ∏ˆŒª…œµƒ ˝ «2£¨æՃл∑∂®![]() µƒ∏ˆŒª…œµƒ ˝ «8£¨110592»•µÙ∫Û3Œªµ√µΩ110£¨
µƒ∏ˆŒª…œµƒ ˝ «8£¨110592»•µÙ∫Û3Œªµ√µΩ110£¨
°þ43£º110£º53£¨
°ý![]() µƒ ÆŒª…œµƒ ˝ «4£¨
µƒ ÆŒª…œµƒ ˝ «4£¨
°ý![]() £ª
£ª
£®2£©”…![]() £¨
£¨![]() £¨æՃл∑∂®
£¨æՃл∑∂®![]() «2Œª ˝£¨”…279841µƒ∏ˆŒª…œµƒ ˝ «1£¨æՃл∑∂®
«2Œª ˝£¨”…279841µƒ∏ˆŒª…œµƒ ˝ «1£¨æՃл∑∂®![]() µƒ∏ˆŒª…œµƒ ˝ «1ªÚ3£¨»Áπ˚ªÆ»•279841∫Û√ʵƒÀƒŒª9841µ√µΩ ˝27£¨∂¯24£º27£º34£¨”…¥Àø…»∑∂®
µƒ∏ˆŒª…œµƒ ˝ «1ªÚ3£¨»Áπ˚ªÆ»•279841∫Û√ʵƒÀƒŒª9841µ√µΩ ˝27£¨∂¯24£º27£º34£¨”…¥Àø…»∑∂®![]() µƒ ÆŒª…œµƒ ˝ «2£¨æ≠—È÷§£¨234=279841£¨
µƒ ÆŒª…œµƒ ˝ «2£¨æ≠—È÷§£¨234=279841£¨
À˘“‘![]() .
.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
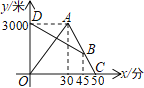
°æƒø°øƒœ…≥»∫µ∫ «Œ“π˙πÔ–¡ÏÕ¡£¨œ÷‘⁄Œ“ƒœ∫£”Ê√Ò“™‘⁄ƒœ…≥ƒ≥∫£µ∫∏ΩΩ¸Ω¯––≤∂”„◊˜“µ£¨µ±”Ê¥¨∫Ω––÷¡B¥¶ ±£¨≤‚µ√∏√µ∫Œª”⁄’˝±±∑ΩœÚ![]() ∫£¿ÔµƒC¥¶£¨Œ™¡À∑¿÷πƒ≥π˙ªπ—≤æØ∏…»≈£¨æիΫی“A¥¶µƒ”„ºý¥¨«∞Õ˘C¥¶ª§∫Ω£¨“—÷™CŒª”⁄A¥¶µƒ±±∆´∂´45°„∑ΩœÚ…œ£¨AŒª”⁄Bµƒ±±∆´Œ˜30°„µƒ∑ΩœÚ…œ£¨«ÛA°¢C÷ƺ‰µƒæý¿Î£Æ
∫£¿ÔµƒC¥¶£¨Œ™¡À∑¿÷πƒ≥π˙ªπ—≤æØ∏…»≈£¨æիΫی“A¥¶µƒ”„ºý¥¨«∞Õ˘C¥¶ª§∫Ω£¨“—÷™CŒª”⁄A¥¶µƒ±±∆´∂´45°„∑ΩœÚ…œ£¨AŒª”⁄Bµƒ±±∆´Œ˜30°„µƒ∑ΩœÚ…œ£¨«ÛA°¢C÷ƺ‰µƒæý¿Î£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº∆À„£∫
£®1£©£®©Å3£©+40+£®©Å32£©+£®©Å8£©
£®2£©12©Å£®©Å18£©+£®©Å7£©
£®3£©£®+3![]() £©©Å£®©Å5
£©©Å£®©Å5![]() £©+£®©Å2
£©+£®©Å2![]() £©©Å£®©Å32
£©©Å£®©Å32![]() £©
£©
£®4£©81.26©Å293.8+8.74+111
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø’≈«Ω®£¨Œ“π˙ƒœ±±≥Ø ±∆⁄£®‘ºπ´‘™5 ¿ºÕ£©÷¯√˚µƒ ˝—ߺ“£¨÷¯”–°∂’≈«Ω®À„æ≠°∑£Æ“ª¥Œ—Áª·…œ£¨’≈«Ω®≥ˆ¡À“ªµ¿Ã‚£∫°∞œ÷”–“ª÷ª¬πœÚŒ˜≈У¨µ±¡‘»À◊∑÷¡![]() ¥¶ ±£¨”άπÀ˘‘⁄µƒ
¥¶ ±£¨”άπÀ˘‘⁄µƒ![]() ¥¶ªπ≤Ó36≤Ω£®π≈¥˙£∫1¿Ô=300≤Ω£©£ª¬πÕª»ªœÚ±±≈У¨¥À ±∆Ԭ̵ƒ¡‘»ÀæÕ—ÿ◊≈
¥¶ªπ≤Ó36≤Ω£®π≈¥˙£∫1¿Ô=300≤Ω£©£ª¬πÕª»ªœÚ±±≈У¨¥À ±∆Ԭ̵ƒ¡‘»ÀæÕ—ÿ◊≈![]() ◊∑»•£¨◊∑¡À50≤Ω÷¡
◊∑»•£¨◊∑¡À50≤Ω÷¡![]() ¥¶”άπÀ˘‘⁄µƒŒª÷√
¥¶”άπÀ˘‘⁄µƒŒª÷√![]() ¥¶ªπ≤Ó10≤Ω£®µ„
¥¶ªπ≤Ó10≤Ω£®µ„![]() °¢
°¢![]() °¢
°¢![]() ‘⁄Õ¨“ª÷±œþ…œ£©£Æ»Áπ˚¥À¬π≤ªœÚ±±◊™£¨∂¯ºÃ–¯œÚŒ˜≈У¨¡‘»À–Ë“™◊∑∂ý‘∂≤≈ƒÐ◊∑…œ¥À¬π£ø°±£¨“—÷™µ•Œª ±º‰ƒ⁄¬π≈еƒ¬∑≥Ã∫Õ¡‘»À∆Ô¬Ì◊∑∏œµƒ¬∑≥õƒ±»÷µ «∂®÷µ£¨«ÎΩ‚¥’‚∏ˆŒ £Æ
‘⁄Õ¨“ª÷±œþ…œ£©£Æ»Áπ˚¥À¬π≤ªœÚ±±◊™£¨∂¯ºÃ–¯œÚŒ˜≈У¨¡‘»À–Ë“™◊∑∂ý‘∂≤≈ƒÐ◊∑…œ¥À¬π£ø°±£¨“—÷™µ•Œª ±º‰ƒ⁄¬π≈еƒ¬∑≥Ã∫Õ¡‘»À∆Ô¬Ì◊∑∏œµƒ¬∑≥õƒ±»÷µ «∂®÷µ£¨«ÎΩ‚¥’‚∏ˆŒ £Æ


≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∫£±ı‘°≥°∂´Œ˜◊þœÚµƒ∫£∞∂œþø…“‘Ω¸À∆ø¥◊˜÷±œþl(»ÁÕº).æ»…˙‘±º◊‘⁄A¥¶µƒ≤tÕ˚î…œπ€≤Ï∫£√Ê«Èøˆ£¨∑¢œ÷∆‰’˝±±∑ΩœÚµƒB¥¶”–»À∑¢≥ˆ«Ûæ»–≈∫≈£¨À˚¡¢º¥—ÿAB∑ΩœÚæ∂÷±«∞Õ˘æ»‘Æ£¨Õ¨ ±Õ®÷™’˝‘⁄∫£∞∂œþ…œ—≤¬þµƒæ»…˙‘±““.““¬Ì…œ¥”C¥¶»Î∫£,æ∂÷±œÚB¥¶”Œ»•.º◊‘⁄““»Î∫£10√Î∫Û∏œµΩ∫£∞∂œþ…œµƒD¥¶,‘ŸœÚB¥¶”Œ»•.»ÙCD=40√◊,B‘⁄Cµƒ±±∆´∂´35°„∑ΩœÚ,º◊““µƒ”Œ”æÀŸ∂»∂º «2√◊/√Î.Œ À≠œ»µΩ¥ÔB¥¶£ø«ÎÀµ√˜¿Ì”….
(≤Œøº ˝æð£∫sin55°„°÷0.82,cos55°„°÷0.57,tan55°„°÷1.43)

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥ÃÏ‘Á≥ø£¨–°ÕØ¥”º“≈Ð≤Ω»•Ã”˝≥°∂Õ¡∂£¨Õ¨ ±–°÷£¥”Ô˝≥°≥ø¡∑Ω· ¯ªÿº“£¨Õæ÷–¡Ω»Àœý”ˆ£Æ–°ÕØ≈еΩÔ˝≥°∫Û∑¢œ÷“™œ¬”Í£¨¡¢º¥∞¥‘≠¬∑∑µªÿ£¨”ˆµΩ–°÷£∫Û¡Ω»À“ª∆ªÿµΩº“£®–°ÕØ∫Õ–°÷£ º÷’‘⁄Õ¨“ªÃı± ÷±µƒπ´¬∑…œ––◊þ£©£Æ»ÁÕº «¡Ω»À¿Îº“µƒæý¿Îy£®√◊£©”Ζ°ÕØ≥ˆ∑¢µƒ ±º‰x£®∑÷£©÷ƺ‰µƒ∫Ø ˝ÕºœÛ£Æµ±x£Ω_______ ±£¨–°ÕؔΖ°÷£œýæý600√◊£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™÷±œþl£∫y£Ω2x£´4Ωªx÷·”⁄A£¨Ωªy÷·”⁄B£Æ

(1) ÷±Ω”–¥≥ˆ÷±œþlœÚ”“∆Ω“∆2∏ˆµ•Œªµ√µΩµƒ÷±œþl1µƒΩ‚Œˆ Ω_______£ª
(2) ÷±Ω”–¥≥ˆ÷±œþlπÿ”⁄y£Ω£≠x∂‘≥∆µƒ÷±œþl2µƒΩ‚Œˆ Ω_______£ª
(3) µ„P‘⁄÷±œþl…œ£¨»ÙS°˜OAP£Ω2S°˜OBP£¨«ÛPµ„◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨π˝±þ≥§Œ™2µƒµ»±þ»˝Ω«–ŒABCµƒ∂•µ„C◊˜÷±œþl°Õ BC£¨»ª∫Û◊˜°˜ABCπÿ”⁄÷±œþl∂‘≥∆µƒ°˜A°‰B°‰C£¨PŒ™œþ∂ŒA°‰C…œ“ª∂ص„£¨¡¨Ω”AP£¨PB£¨‘ÚAP£´PBµƒ◊Ó–°÷µ « £® £©
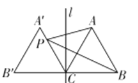
A.4B.3C.2D.2£´![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒœ≈£¥”ƒ≥µ„Oø™ º—ÿ∂´Œ˜∑ΩœÚ÷±œþ≈¿––£¨πÊ∂®œÚ∂´≈¿––µƒ¬∑≥ú«Œ™’˝ ˝£¨œÚŒ˜≈¿––µƒ¬∑≥ú«Œ™∏∫ ˝£Æ≈¿––µƒ∏˜∂Œ¬∑≥Ó¿¥ŒŒ™£®µ•Œª£∫¿Â√◊£©£∫![]() .Œ £∫
.Œ £∫
£®1£©Œœ≈£◊Ó∫Û «∑ÒªÿµΩ≥ˆ∑¢µ„O£ø
£®2£©Œœ≈£¿Îø™≥ˆ∑¢µ„O◊Ó‘∂ «∂ý…Ÿ¿Â√◊£ø
£®3£©‘⁄≈¿––π˝≥Ã÷–£¨»Áπ˚√ø≈¿––1¿Â√◊Ω±¿¯“ª¡£÷•¬È£¨‘ÚŒœ≈£ø…µ√µΩ∂ý…Ÿ¡£÷•¬È£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com