
【题目】如图,已知正比例函数y![]() =ax的图象与反比例函数
=ax的图象与反比例函数![]() 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2).
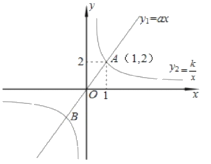
(1)求这两个函数表达式;
(2)根据图象写出正比例函数值大于反比例函数值的x的取值范围;
(3)根据反比例函数的图象,写出当2<x<1时y![]() 的取值范围。
的取值范围。
【答案】(1)y![]() =2x,y
=2x,y![]() =
=![]() .(2)1<x<0或x>1.(3)2<y
.(2)1<x<0或x>1.(3)2<y![]() <1
<1
【解析】
(1)根据点A的坐标,利用待定系数法即可求出正(反)比例函数表达式;
(2)由两函数图象的对称性可得出点B的坐标,再根据两函数图象的上下位置关系,即可找出正比例函数值大于反比例函数值的x的取值范围;
(3)根据反比例函数的性质找出在-2<x<-1上,y值随x值的增大而减小,再根据反比例函数图象上点的坐标特征,即可找出当-2<x<-1时y![]() 的取值范围.
的取值范围.
(1)将点A(1,2)代入y![]() =ax中,
=ax中,
2=a×1,解得:a=2,
∴正比例函数表达式为y![]() =2x.
=2x.
将点A(1,2)代入![]() 中,
中,
2=![]() ,解得:k=2,
,解得:k=2,
∴反比例函数表达式为y![]() =
=![]() .
.
(2)由正、反比例函数图象的对称性可知:点B的坐标为(1,2).
观察函数图象可知:当1<x<0或x>1时,正比例函数图象在反比例函数图象上方,
∴正比例函数值大于反比例函数值的x的取值范围为1<x<0或x>1.
(3)∵k=2>0,
∴在2<x<1上,y值随x值的增大而减小。
当x=2时,y![]() =
=![]() =1;
=1;
当x=1时,y![]() =
=![]() =2.
=2.
∴当2<x<1时y![]() 的取值范围为2<y
的取值范围为2<y![]() <1.
<1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题:
例题:已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),则x2-4x+m=x2+(n+3)x+3n.
∴![]() ,
,
解得:![]() .
.
∴另一个因式为(x-7),m的值为-21.
问题:仿照以上方法解答下面问题:
(1)已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值
(2)已知二次三项式6x2+4ax+2有一个因式是(2x+a),a是正整数,求另一个因式以及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织全体学生参加“献爱心”公益活动,为了了解九年级学生参加活动情况,从九年级学生着中随机抽取部分学生进行调查,统计了该天他们打扫街道,去敬老院服务和到社区文艺演出的人数,并绘制了如下不完整的条形统计图和扇形统计图,其中到社区文艺演出的人数占所调查的九年级学生人数的![]() ,请根据两幅统计图中的信息,回答下列问题:
,请根据两幅统计图中的信息,回答下列问题:
(1)本次调查共抽取了多少名九年级学生?
(2)补全条形统计图.
(3)若该中学九年级共有1500名学生,请你估计该中学九年级去敬老院的学生有多少名?
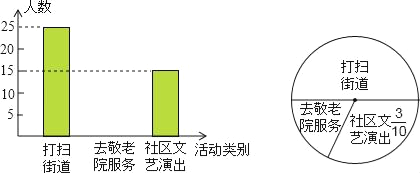
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
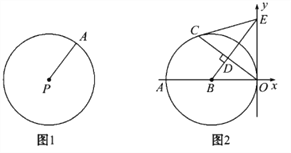
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心, ![]() 为半径的圆的方程为:________;
为半径的圆的方程为:________;
(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
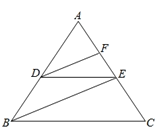
如图,已知:DE∥BC,DF、BE分别平分∠ADE、∠ABC.
求证:∠FDE=∠DEB
证明:∵DE∥BC(已知)
∴∠ADE=∠ ① ( ② )
∵DF、BE分别平分∠ADE、∠ABC,(已知)
∴∠ADF=![]() ∠ ③ ( ④ )
∠ ③ ( ④ )
∠ABE=![]() ∠ ⑥ ( ⑤ )
∠ ⑥ ( ⑤ )
∴∠ADF=∠ABE(等量代换)
∴DF∥ ( ⑦ )
∴∠FDE=∠DEB( ⑧ )
查看答案和解析>>
科目:初中数学 来源: 题型:
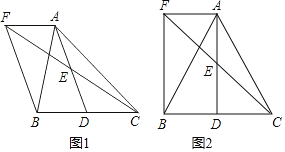
【题目】如图1,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:点D是线段BC的中点;
(2)如图2,若AB=AC=13,AF=BD=5,求四边形AFBD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为1个单位的正方形网格图中,建立了平面直角坐标系xOy,按要求解答下列问题:

(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后得到的图形△A1B1C1;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com