
【题目】仔细阅读下面例题,解答问题:
例题:已知二次三项式x2-4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),则x2-4x+m=x2+(n+3)x+3n.
∴![]() ,
,
解得:![]() .
.
∴另一个因式为(x-7),m的值为-21.
问题:仿照以上方法解答下面问题:
(1)已知二次三项式2x2+3x-k有一个因式是(2x-5),求另一个因式以及k的值
(2)已知二次三项式6x2+4ax+2有一个因式是(2x+a),a是正整数,求另一个因式以及a的值.
【答案】(1)另一个因式是:x+4,k=20.(2)另一个因式是3x+1,a的值是2.
【解析】
(1)设另一个因式是(x+b),则(2x-5)(x+b)=2x2+2bx-5x-5b=2x2+(2b-5)x-5b=2x2+3x-k,根据对应项的系数相等即可求得b和k的值;
(2)设另一个因式是(3x+m),利用多项式的乘法运算法则展开,然后根据对应项的系数相等列式求出m、a的值,然后代入代数式进行计算即可得解.
(1)设另一个因式是(x+b),则
(2x-5)(x+b)=2x2+2bx-5x-5b=2x2+(2b-5)x-5b=2x2+3x-k,
则![]() ,
,
解得:![]() .
.
则另一个因式是:x+4,k=20.
(2)设另一个因式是(3x+m),则
(2x+a)(3x+m)=6x2+(2m+3a)x+am=6x2+4ax+2,
则![]() ,
,
解得![]() 或
或![]() ,
,
另一个因式是3x-1,a的值是-2(不合题意舍去),
故另一个因式是3x+1,a的值是2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探索:将连续的奇数 1,3,5,7…排列成如下的数表,用十字框框出 5 个数(如图)
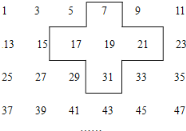
(1)若将十字框上下左右平移,但一定要框住数列中的 5 个数,若设中间的数为 a,用 a 的代数式表示十字框框住的 5 个数字之和;
(2)十字框框住的 5 个数之和能等于 285 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由;
(3)十字框框住的 5 个数之和能等于 365 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】回答下列问题:
(1)如图所示的甲、乙两个平面图形能折什么几何体?
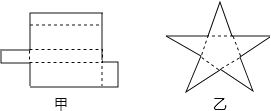
(2)由多个平面围成的几何体叫做多面体.若一个多面体的面数为f,顶点个数为v,棱数为e,分别计算第(1)题中两个多面体的f+v﹣e的值?你发现什么规律?
(3)应用上述规律解决问题:一个多面体的顶点数比面数大8,且有50条棱,求这个几何体的面数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y![]() =ax的图象与反比例函数
=ax的图象与反比例函数![]() 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2).
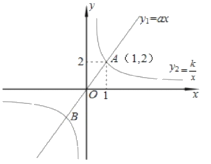
(1)求这两个函数表达式;
(2)根据图象写出正比例函数值大于反比例函数值的x的取值范围;
(3)根据反比例函数的图象,写出当2<x<1时y![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() ,
,![]() 对应的数分别为
对应的数分别为![]() ,8.
,8.
(1)如图1,如果点![]() 和点
和点![]() 分别从点
分别从点![]() ,
,![]() 同时出发,沿数轴负方向运动,点
同时出发,沿数轴负方向运动,点![]() 的运动速度为每秒2个单位,点
的运动速度为每秒2个单位,点![]() 的运动速度为每秒6个单位.
的运动速度为每秒6个单位.

①![]() ,
,![]() 两点之间的距离为__________.
两点之间的距离为__________.
②当![]() ,
,![]() 两点相遇时,点
两点相遇时,点![]() 在数轴上对应的数是____________.
在数轴上对应的数是____________.
③求点![]() 出发多少秒后,与点
出发多少秒后,与点![]() 之间相距4个单位长度?
之间相距4个单位长度?
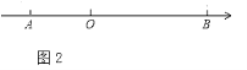
(2)如图2,如果点![]() 从点
从点![]() 出发沿数轴的正方向以每秒2个单位的速度运动,点
出发沿数轴的正方向以每秒2个单位的速度运动,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,在运动过程中,线段
的中点,在运动过程中,线段![]() 的长度是否为定值.如果变化,请说明理由:如果不变,请直接写出线段
的长度是否为定值.如果变化,请说明理由:如果不变,请直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com