
【题目】完成下面推理过程:
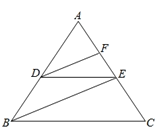
如图,已知:DE∥BC,DF、BE分别平分∠ADE、∠ABC.
求证:∠FDE=∠DEB
证明:∵DE∥BC(已知)
∴∠ADE=∠ ① ( ② )
∵DF、BE分别平分∠ADE、∠ABC,(已知)
∴∠ADF=![]() ∠ ③ ( ④ )
∠ ③ ( ④ )
∠ABE=![]() ∠ ⑥ ( ⑤ )
∠ ⑥ ( ⑤ )
∴∠ADF=∠ABE(等量代换)
∴DF∥ ( ⑦ )
∴∠FDE=∠DEB( ⑧ )
【答案】①∠ABC;②两直线平行,同位角相等;③∠ADE,④角平分线定义;⑤角平分线定义;⑥∠ABC; ⑦BE,同位角相等,两直线平行;⑧DEB,两直线平行,内错角相等
【解析】
根据平行线的性质由DE∥BC得∠ADE=∠ABC,再根据角平分线的定义得到∠ADF=![]() ∠ADE,∠ABE=
∠ADE,∠ABE=![]() ∠ABC,则∠ADF=∠ABE,然后根据平行线的判定得到DF∥BE,最后利用平行线的性质得∠FDE=∠DEB.
∠ABC,则∠ADF=∠ABE,然后根据平行线的判定得到DF∥BE,最后利用平行线的性质得∠FDE=∠DEB.
∵DE∥BC,(已知)
∴∠ADE=∠ABC,(两直线平行,同位角相等)
∵DF、BE分别平分∠ADE、∠ABC,(已知)
∴∠ADF=![]() ∠ADE,(角平分线定义)
∠ADE,(角平分线定义)
∠ABE=![]() ∠ABC,(角平分线定义)
∠ABC,(角平分线定义)
∴∠ADF=∠ABE,(等量代换)
∴DF∥BE,(同位角相等,两直线平行)
∴∠FDE=∠DEB.(两直线平行,内错角相等)


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y![]() =ax的图象与反比例函数
=ax的图象与反比例函数![]() 的图象有一个公共点A(1,2).
的图象有一个公共点A(1,2).
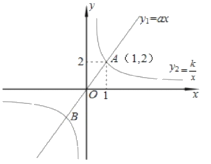
(1)求这两个函数表达式;
(2)根据图象写出正比例函数值大于反比例函数值的x的取值范围;
(3)根据反比例函数的图象,写出当2<x<1时y![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.
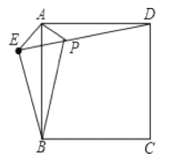
(1)求证:△APD≌△AEB;
(2)连接PC,求线段PC的长度;
(3)试求正方形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果![]() ,那么
,那么![]() 的值是( )
的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() ,
,![]() 对应的数分别为
对应的数分别为![]() ,8.
,8.
(1)如图1,如果点![]() 和点
和点![]() 分别从点
分别从点![]() ,
,![]() 同时出发,沿数轴负方向运动,点
同时出发,沿数轴负方向运动,点![]() 的运动速度为每秒2个单位,点
的运动速度为每秒2个单位,点![]() 的运动速度为每秒6个单位.
的运动速度为每秒6个单位.

①![]() ,
,![]() 两点之间的距离为__________.
两点之间的距离为__________.
②当![]() ,
,![]() 两点相遇时,点
两点相遇时,点![]() 在数轴上对应的数是____________.
在数轴上对应的数是____________.
③求点![]() 出发多少秒后,与点
出发多少秒后,与点![]() 之间相距4个单位长度?
之间相距4个单位长度?
(2)如图2,如果点![]() 从点
从点![]() 出发沿数轴的正方向以每秒2个单位的速度运动,点
出发沿数轴的正方向以每秒2个单位的速度运动,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点,在运动过程中,线段
的中点,在运动过程中,线段![]() 的长度是否为定值.如果变化,请说明理由:如果不变,请直接写出线段
的长度是否为定值.如果变化,请说明理由:如果不变,请直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
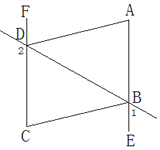
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)求证:BC平分∠DBE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com