
【题目】已知:如图,在正方形ABCD外取点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P,已知AE=AP=BE=1.
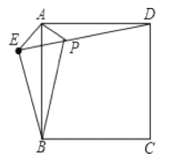
(1)求证:△APD≌△AEB;
(2)连接PC,求线段PC的长度;
(3)试求正方形ABCD的面积。
【答案】(1)见解析(2)![]() (3)2+
(3)2+![]()
【解析】
(1)由四边形ABCD是正方形,得到AB=AD,∠BAD=90°,由AE⊥AP,得到∠EAP=90°,于是得到∠EAB=∠DAP,即可得到结论;
(2)连接PB,PC,由(1)证得△APD≌△AEB,于是得到PD=AE,∠ADO=∠ABE,推出△ABP≌△DCP,得到PB=PC,根据勾股定理即可得到结论;
(3)过A作AM⊥PE于M,根据等腰直角三角形的性质得到AM=PM=![]() ,求出DM=1+
,求出DM=1+![]() ,由勾股定理得到AD=
,由勾股定理得到AD=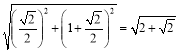 ,于是得到结果.
,于是得到结果.
(1)∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE⊥AP,
∴∠EAP=90°,
∴∠EAB=∠DAP,
在△APD与△AEB中,
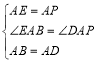 ,
,
∴△APD≌△AEB;
(2)连接PB,PC,由(1)证得△APD≌△AEB,
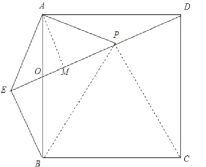
∴PD=AE,∠ADO=∠ABE,
∵AE=AP,
∴PD=AP,
∴∠PAD=∠PDA,
∴∠BAP=∠CDP,
在△ABP与△DCP中,
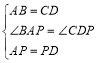 ,
,
∴△ABP≌△DCP,
∴PB=PC,
∵∠BOE=∠AOP,
∴∠BEO=∠BAD=90°,
∵PE=![]() AP=
AP=![]() ,
,
∴PB=![]() ,
,
∴PC=PB=![]() ;
;
(3)过A作AM⊥PE于M,
∴AM=PM=![]() PE=
PE=![]() ,
,
∴DM=1+![]() ,
,
∴AD=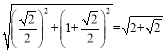 ,
,
∴正方形ABCD的面积=AD![]() =2+
=2+![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为![]() 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人![]() 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过![]() 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:
(1)如果去乙草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(2)如果![]() 个人去甲草莓园采摘
个人去甲草莓园采摘![]() 千克草莓,需支付多少元?
千克草莓,需支付多少元?
(3)小颖和妈妈准备采摘![]() 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
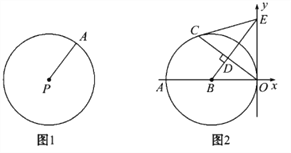
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心, ![]() 为半径的圆的方程为:________;
为半径的圆的方程为:________;
(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
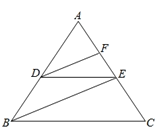
如图,已知:DE∥BC,DF、BE分别平分∠ADE、∠ABC.
求证:∠FDE=∠DEB
证明:∵DE∥BC(已知)
∴∠ADE=∠ ① ( ② )
∵DF、BE分别平分∠ADE、∠ABC,(已知)
∴∠ADF=![]() ∠ ③ ( ④ )
∠ ③ ( ④ )
∠ABE=![]() ∠ ⑥ ( ⑤ )
∠ ⑥ ( ⑤ )
∴∠ADF=∠ABE(等量代换)
∴DF∥ ( ⑦ )
∴∠FDE=∠DEB( ⑧ )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B两个蔬菜市场各有蔬菜14吨,现要全部运往甲、乙两地,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从蔬菜市场A到甲地运费50元/吨,到乙地30元/吨;从蔬菜市场B到甲地运费60元/吨,到乙地45元/吨。
(1)设从蔬菜市场A向甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
蔬菜市场A | x | |
蔬菜市场B |
(2)若总运费为1300元,则从蔬菜市场A向甲地运送蔬菜多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,D是BC边上一点,E是AD的中点,过点A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:点D是线段BC的中点;
(2)如图2,若AB=AC=13,AF=BD=5,求四边形AFBD的面积.
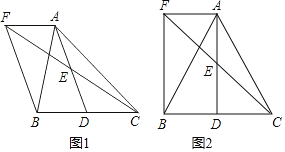
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有依次3个数:2、9、7.对任意相邻的两个数,都用右边的数减去左边的数,所得之差写在这两个数之间,可产生一个新数串:2、7、9、-2、7,这称为第1次操作,做第2次同样的操作后也可以产生一个新数串:2、5、7、2、9、-11、-2、9、7,继续依次操作下去,问从数串2、9、7开始操作第20次后所产生的那个数串的所有数之和是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠A0B=420,点P为∠A0B内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为________,∠MPN ________.
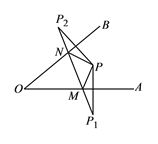
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com