
如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,PN+PM+MN的最小值是5cm,则∠AOB的度数是__________.
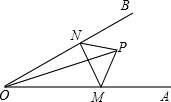
30°.
【考点】轴对称-最短路线问题.
【分析】分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,由对称的性质得出PM=CM,OP=OC,∠COA=∠POA;PN=DN,OP=OD,∠DOB=∠POB,得出∠AOB=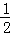 ∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.
【解答】解:分别作点P关于OA、OB的对称点C、D,连接CD,
分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如 图所示:
图所示:
∵点P关于OA的对称点为D,关于OB的对称点为C,
∴PM=DM,OP=OD,∠DOA=∠POA;
∵点P关于OB的对称点为C,
∴PN=CN,OP=OC,∠COB=∠POB,
∴OC=OP=OD,∠AOB=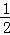 ∠COD,
∠COD,
∵PN+PM+MN的最小值是5cm,
∴PM+PN+MN=5,
∴DM+CN+MN=5,
即CD=5=OP,
∴OC=OD=CD,
即△OCD是等边三角形,
∴∠COD=60°,
∴∠AOB=30°.
故答案为:30°.

【点评】本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质;熟练掌握轴对称的性质, 证明三角形是等边三角形是解决问题的关键.
证明三角形是等边三角形是解决问题的关键.


 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
如图,如果把△ABC的顶点A先向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )

A.垂直 B.相等 C.平分 D.平分且垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
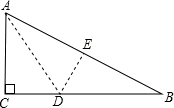
如图,有一块直角三角形纸片,两直角边AC=3cm,BC=4cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
下列语句中正确的有( )句
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com