
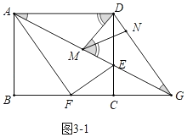
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 边上一点,连接
边上一点,连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,顶点
折叠,顶点![]() 恰好落在
恰好落在![]() 边上点
边上点![]() 处,延长
处,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求线段![]() 的长;
的长;
(2)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点(与端点不重合),且
上的动点(与端点不重合),且![]() .
.
①求证:![]() ∽
∽![]() ;
;
②是否存在这样的点![]() ,使
,使![]() 是等腰三角形?若存在,请求出
是等腰三角形?若存在,请求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

【答案】(1)3;(2)①见解析;②存在.由①得△DMN∽△DGM,理由见解析
【解析】
(1)根据矩形的性质和折叠的性质得出AD=AF、DE=EF,进而设EC=x,则DE=EF=8﹣x,利用勾股定理求解即可得出答案;
(2)①根据平行线的性质得出△DAE∽△CGE求得CG=6,进而根据勾股定理求出DG=10,得出AD=DG,即可得出答案;②假设存在,由①可得当△DGM是等腰三角形时△DMN是等腰三角形,分两种情况进行讨论:当MG=DG=10时,结合勾股定理进行求解;当MG=DM时,作MH⊥DG于H,证出△GHM∽△GBA,即可得出答案.
解:(1)如图1中,∵四边形ABCD是矩形,
∴AD=BC=10,AB=CD=8,∠B=∠BCD =∠D=90°,
由翻折可知:AD=AF=10.DE=EF,设EC=x,则DE=EF=8﹣x.
在Rt△ABF中,BF=![]() =6,
=6,
∴CF=BC﹣BF=10﹣6=4,
在Rt△EFC中,则有:(8﹣x)2=x2+42,
∴x=3,
∴EC=3.
(2)①如图2中,
∵AD∥CG,
∴∠DAE=∠CGE,∠ADE=∠GCE
∴△DAE∽△CGE
∴![]() =
=![]() ,
,
∴![]() ,
,
∴CG=6,
∴在Rt△DCG中,![]() ,
,
∴AD=DG
∴∠DAG=∠AGD,
∵∠DMN=∠DAM
∴∠DMN=∠DGM
∵∠MDN=∠GDM
∴△DMN∽△DGM
②存在.由①得△DMN∽△DGM
∴当△DGM是等腰三角形时△DMN是等腰三角形
有两种情形:
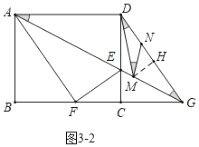
如图3﹣1中,当MG=DG=10时,
∵BG=BC+CG=16,
∴在Rt△ABG中,![]() ,
,
∴AM=AG - MG = ![]() .
.
如图3﹣2中,当MG=DM时,作MH⊥DG于H.
∴DH=GH=5,
由①得∠DGM =∠DAG=∠AGB
∵∠MHG =∠B
∴△GHM∽△GBA
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
综上所述,AM的长为![]() 或
或![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
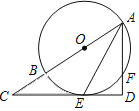
【题目】如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线;
(2)∠C=45°,⊙O的半径为2,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场某种商品平均每天可销售![]() 件,每件盈利
件,每件盈利![]() 元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价
元,为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价![]() 元,商场平均每天可多售出
元,商场平均每天可多售出![]() 件,设每件商品降价
件,设每件商品降价![]() 元(
元(![]() 为正整数).据此规律,请回答:
为正整数).据此规律,请回答:
(1)商场日销轡量增加 件,每件商品盈利 元(用含![]() 的代数式表示);
的代数式表示);
(2)每件商品降价多少元时,商场日盈利可达到![]() 元;
元;
(3)在上述条件不变,销售正常情况下,求商场日盈利的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
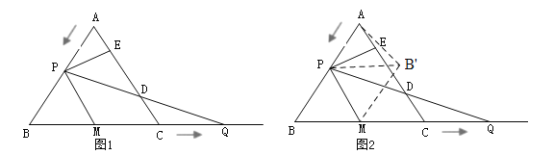
【题目】如图1,在等边![]() 中,
中,![]() ,动点
,动点![]() 从点
从点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 匀速运动,动点
匀速运动,动点![]() 同时从点
同时从点![]() 出发以同样的速度沿
出发以同样的速度沿![]() 的延长线方向匀速运动,当点
的延长线方向匀速运动,当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动.设运动时间为
同时停止运动.设运动时间为![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,
,![]() 交
交![]() 边于
边于![]() ,线段
,线段![]() 的中点为
的中点为![]() ,连接
,连接![]() .
.
(1)当![]() 为何值时,
为何值时,![]() 与
与![]() 相似;
相似;
(2)在点![]() 、
、![]() 运动过程中,点
运动过程中,点![]() 、
、![]() 也随之运动,线段
也随之运动,线段![]() 的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求
的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求![]() 的长;
的长;
(3)如图2,将![]() 沿直线
沿直线![]() 翻折,得
翻折,得![]() ,连接
,连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 的值最小?并求出最小值.
的值最小?并求出最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,则树高_____________米(结果保留根号).
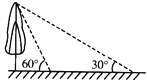
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有三个标记为1,2,3的小球(材质、形状、大小等完全相同),甲先从中随机取出一个小球,记下数字为![]() 后放回,同样的乙也从中随机取出一个小球,记下数字为
后放回,同样的乙也从中随机取出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)请用列表或画树状图的方法写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求点![]() 在函数
在函数![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AC=13,BC=5,BE⊥DC交DC的延长线于点E.

(1)求证:CB是∠ECA的角平分线;
(2)求DE的长;
(3)求证:BE是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
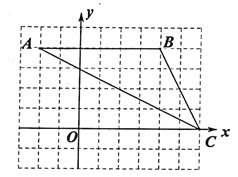
【题目】如图,在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)![]() 的面积是_______;
的面积是_______;
(2)请以原点![]() 为位似中心,画出
为位似中心,画出![]() ,使它与
,使它与![]() 的相似比为
的相似比为![]() ,变换后点
,变换后点![]() 的对应点分别为点
的对应点分别为点![]() ,点
,点![]() 在第一象限;
在第一象限;
(3)若![]() 为线段
为线段![]() 上的任一点,则变换后点
上的任一点,则变换后点![]() 的对应点
的对应点![]() 的坐标为 _______.
的坐标为 _______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com