
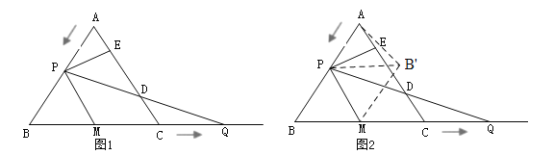
ĄŸÌâÄżĄżÈçÍŒ1ŁŹÔڔȱß![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹ¶Ż”ă
ŁŹ¶Ż”ă![]() ŽÓ”ă
ŽÓ”ă![]() łö·ąÒÔ
łö·ąÒÔ![]() ”ÄËÙ¶ÈŃŰ
”ÄËÙ¶ÈŃŰ![]() ÔÈËÙÔ˶ŻŁŹ¶Ż”ă
ÔÈËÙÔ˶ŻŁŹ¶Ż”ă![]() ÍŹÊ±ŽÓ”ă
ÍŹÊ±ŽÓ”ă![]() łö·ąÒÔÍŹŃù”ÄËÙ¶ÈŃŰ
łö·ąÒÔÍŹŃù”ÄËÙ¶ÈŃŰ![]() ”ÄŃÓł€Ïß·œÏòÔÈËÙÔ˶ŻŁŹ”±”ă
”ÄŃÓł€Ïß·œÏòÔÈËÙÔ˶ŻŁŹ”±”ă![]() ”œŽï”ă
”œŽï”ă![]() ʱŁŹ”ă
ʱŁŹ”ă![]() Ąą
Ąą![]() ÍŹÊ±ÍŁÖčÔ˶ŻŁźÉèÔ˶ŻÊ±ŒäÎȘ
ÍŹÊ±ÍŁÖčÔ˶ŻŁźÉèÔ˶ŻÊ±ŒäÎȘ![]() ŁŹčę”ă
ŁŹčę”ă![]() Śś
Śś![]() ÓÚ
ÓÚ![]() ŁŹ
ŁŹ![]() œ»
œ»![]() ±ßÓÚ
±ßÓÚ![]() ŁŹÏ߶Î
ŁŹÏ߶Î![]() ”ÄÖĐ”ăÎȘ
”ÄÖĐ”ăÎȘ![]() ŁŹÁŹœÓ
ŁŹÁŹœÓ![]() Łź
Łź
Łš1Ł©”±![]() ÎȘșÎ֔ʱŁŹ
ÎȘșÎ֔ʱŁŹ![]() Óë
Óë![]() ÏàËÆŁ»
ÏàËÆŁ»
Łš2Ł©ÔÚ”ă![]() Ąą
Ąą![]() Ô˶ŻčęłÌÖĐŁŹ”ă
Ô˶ŻčęłÌÖĐŁŹ”ă![]() Ąą
Ąą![]() ÒČËæÖźÔ˶ŻŁŹÏ߶Î
ÒČËæÖźÔ˶ŻŁŹÏ߶Î![]() ”Äł€¶ÈÊÇ·ń»á·ąÉú±ä»ŻŁżÈô·ąÉú±ä»ŻŁŹÇë˔ÜÀíÓÉŁŹÈôČ»·ąÉú±ä»ŻŁŹÇó
”Äł€¶ÈÊÇ·ń»á·ąÉú±ä»ŻŁżÈô·ąÉú±ä»ŻŁŹÇë˔ÜÀíÓÉŁŹÈôČ»·ąÉú±ä»ŻŁŹÇó![]() ”Äł€Ł»
”Äł€Ł»
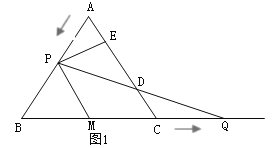
Łš3Ł©ÈçÍŒ2ŁŹœ«![]() ŃŰÖ±Ïß
ŃŰÖ±Ïß![]() ·ŐÛŁŹ”Ă
·ŐÛŁŹ”Ă![]() ŁŹÁŹœÓ
ŁŹÁŹœÓ![]() ŁŹ”±
ŁŹ”±![]() ÎȘșÎ֔ʱŁŹ
ÎȘșÎ֔ʱŁŹ![]() ”ÄÖ”ŚîĐĄŁżČąÇółöŚîĐĄÖ”Łź
”ÄÖ”ŚîĐĄŁżČąÇółöŚîĐĄÖ”Łź
ĄŸŽđ°žĄżŁš1Ł©3Ł»Łš2Ł©Č»±ä»ŻŁŹ3cmŁ»Łš3Ł©![]() ŁŹŚîĐĄÖ”
ŁŹŚîĐĄÖ”![]()
ĄŸœâÎöĄż
Łš1Ł©žùŸĘÌâÒâ”±![]() ŁŹ
ŁŹ![]() ŁŹčÊżÉÇóœâŁ»
ŁŹčÊżÉÇóœâŁ»
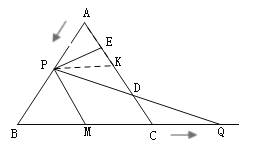
Łš2Ł©Śś![]() œ»
œ»![]() ÓÚ
ÓÚ![]() ŁŹ”Ă”œ
ŁŹ”Ă”œ![]() ÊǔȱßÈęœÇĐÎŁŹ
ÊǔȱßÈęœÇĐÎŁŹ![]() ŁŹAE=EKŁŹÔÙրÜ
ŁŹAE=EKŁŹÔÙրÜ![]() ŁŹ”Ă”œ
ŁŹ”Ă”œ![]() ŁŹÀûÓĂ
ŁŹÀûÓĂ![]() ŒŽżÉÇóœâŁ»
ŒŽżÉÇóœâŁ»
Łš3Ł©ÁŹœÓ![]() ŁŹ
ŁŹ![]() ŁŹżÉ”Ă
ŁŹżÉ”Ă![]() ,ÓÉ
,ÓÉ![]() żÉÖȘ”±
żÉÖȘ”±![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÔÚÒ»ÌőÖ±ÏßÉÏʱŁŹ
ÔÚÒ»ÌőÖ±ÏßÉÏʱŁŹ![]() ŚîĐĄŁŹÔÙžùŸĘŐÛ”ț”ÄĐÔÖÊŒ°čŽčɶšÀ팎żÉÇółö
ŚîĐĄŁŹÔÙžùŸĘŐÛ”ț”ÄĐÔÖÊŒ°čŽčɶšÀ팎żÉÇółö![]() ”ÄŚîĐĄÖ”.
”ÄŚîĐĄÖ”.
œâŁșŁš1Ł©![]() ÊǔȱßÈęœÇĐÎŁŹ
ÊǔȱßÈęœÇĐÎŁŹ
Ąà![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
ĄàÖ»ÓĐ”±![]() ʱ,
ʱ,![]() ,
,
Ôò![]() ŁŹ
ŁŹ![]() ÊÇ
ÊÇ![]() ”ÄÖД㣏
”ÄÖД㣏
![]() ÊÇ
ÊÇ![]() ”ÄÖД㣏
”ÄÖД㣏
ŒŽ![]() ,
,
![]() ʱŁŹ
ʱŁŹ![]() Ł»
Ł»
Łš2Ł©Č»±ä»Ż.ÀíÓÉÈçÏÂŁș
ÈçÍŒ2ÖĐŁŹŚś![]() œ»
œ»![]() ÓÚ
ÓÚ![]() .
.
![]() ÊǔȱßÈęœÇĐÎŁŹ
ÊǔȱßÈęœÇĐÎŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() ,
,
![]() ÊǔȱßÈęœÇĐÎŁŹ
ÊǔȱßÈęœÇĐÎŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
ĄàAE=EKŁŹ
![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]()
Łš3Ł©ÈçÍŒ3ÖĐŁŹÁŹœÓ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
Ôò![]() ,
,
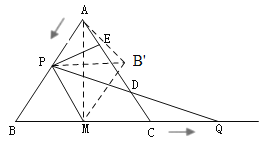
¶ű![]() ŁŹ
ŁŹ
Ąà”±![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÔÚÒ»ÌőÖ±ÏßÉÏʱŁŹ
ÔÚÒ»ÌőÖ±ÏßÉÏʱŁŹ![]() ŚîĐĄŁŹ
ŚîĐĄŁŹ
![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ
![]() ,
,
![]() ŁŹ
ŁŹ
![]() ŁŹ
ŁŹ
![]() ”ÄŚîĐĄÖ”ÎȘ
”ÄŚîĐĄÖ”ÎȘ![]() .
.



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÔĶÁÒÔÏÂČÄÁÏŁŹČą°ŽÒȘÇóÍêłÉÏàÓŠ”ŰÈÎÎńŁș
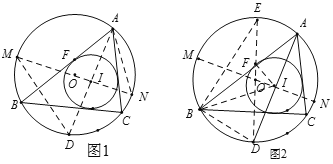
Àł°șčț”ÂĄ€Ć·À(Leonhard Euler)ÊÇÈđÊżÊęѧŒÒŁŹÔÚÊęѧÉÏŸłŁŒû”œÒÔËû”ÄĂûŚÖĂüĂû”ÄÖŰÒȘłŁÊ꣏č«ÊœșͶšÀíŁŹÏÂĂæÊÇĆ·À·ąÏÖ”ÄÒ»žö¶šÀíŁșÔÚĄśABCÖĐŁŹRșÍr·Ö±đÎȘÍâœÓÔČșÍÄÚÇĐÔČ”Ä°ëŸ¶ŁŹOșÍI·Ö±đÎȘÆäÍâĐÄșÍÄÚĐÄŁŹÔò![]() .
.
ÈçÍŒ1ŁŹĄŃOșÍĄŃI·Ö±đÊÇĄśABC”ÄÍâœÓÔČșÍÄÚÇĐÔČŁŹĄŃIÓëABÏàÇĐ·ÖÓÚ”ăFŁŹÉèĄŃO”İ럶ÎȘRŁŹĄŃI”İ럶ÎȘrŁŹÍâĐÄOŁšÈęœÇĐÎÈę±ßŽčֱƜ·ÖÏߔĜ»”㣩ÓëÄÚĐÄIŁšÈęœÇĐÎÈęÌőœÇÆœ·ÖÏߔĜ»”㣩֟Œä”ÄŸàÀëOIŁœdŁŹÔòÓĐd2ŁœR2©2RrŁź
ÏÂĂæÊǞöšÀí”ÄրÜčęłÌŁšČż·ÖŁ©Łș
ŃÓł€AIœ»ĄŃOÓÚ”ăDŁŹčę”ăIŚśĄŃO”ÄÖ±Ÿ¶MNŁŹÁŹœÓDMŁŹAN.
ĄßĄÏD=ĄÏNŁŹĄÏDMI=ĄÏNAI(ÍŹ»ĄËù¶Ô”ÄÔČÖÜœÇÏà”È)ŁŹ
ĄàĄśMDIĄŚĄśANIŁŹ
Ąà![]() ŁŹ
ŁŹ
Ąà![]() ąÙŁŹ
ąÙŁŹ
ÈçÍŒ2ŁŹÔÚÍŒ1(ÒțÈ„MDŁŹAN)”Ä»ùŽĄÉÏŚśĄŃO”ÄÖ±Ÿ¶DEŁŹÁŹœÓBEŁŹBDŁŹBIŁŹIFŁŹ
ĄßDEÊÇĄŃO”ÄÖ±Ÿ¶ŁŹĄàĄÏDBE=90ĄăŁŹ
ĄßĄŃIÓëABÏàÇĐÓÚ”ăFŁŹĄàĄÏAFI=90ĄăŁŹ
ĄàĄÏDBE=ĄÏIFAŁŹ
ĄßĄÏBAD=ĄÏE(ÍŹ»ĄËù¶ÔÔČÖÜœÇÏà”È)ŁŹ
ĄàĄśAIFĄŚĄśEDBŁŹ
Ąà![]() ŁŹĄà
ŁŹĄà![]() ąÚŁŹ
ąÚŁŹ
ÈÎÎńŁș(1)čÛČì·ąÏÖŁș![]() ŁŹ
ŁŹ![]() (ÓĂșŹRŁŹd”ÄŽúÊęÊœ±íÊŸ)Ł»
(ÓĂșŹRŁŹd”ÄŽúÊęÊœ±íÊŸ)Ł»
(2)ÇëĆжÏBDșÍID”ÄÊęÁżčŰÏ”ŁŹČąË”ĂśÀíÓÉŁ»
(3)ÇëčÛČìÊœŚÓąÙșÍÊœŚÓąÚŁŹČąÀûÓĂÈÎÎń(1)ŁŹ(2)”ÄœáÂÛŁŹ°ŽŐŐÉÏĂæ”ÄÖ€ĂśËŒÂ·ŁŹÍêłÉžĂ¶šÀíրÜ”ÄÊŁÓàČż·ÖŁ»
(4)ÓŠÓĂŁșÈôĄśABC”ÄÍâœÓÔČ”Ä°ëŸ¶ÎȘ5cmŁŹÄÚÇĐÔČ”Ä°ëŸ¶ÎȘ2cmŁŹÔòĄśABC”ÄÍâĐÄÓëÄÚĐÄÖźŒä”ÄŸàÀëÎȘ cm.

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒ»ŽÎșŻÊęyŁœx+4”ÄÍŒÏóÓë·Ž±ÈÀęșŻÊęyŁœ![]() ŁškÎȘłŁÊęÇÒkĄÙ0Ł©”ÄÍŒÏóœ»ÓÚAŁš©1ŁŹ3Ł©ŁŹBŁšbŁŹ1Ł©Áœ”㣟
ŁškÎȘłŁÊęÇÒkĄÙ0Ł©”ÄÍŒÏóœ»ÓÚAŁš©1ŁŹ3Ł©ŁŹBŁšbŁŹ1Ł©Áœ”㣟
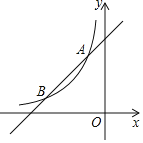
Łš1Ł©Ç󷎱ÈÀęșŻÊę”ıíŽïÊœŁ»
Łš2Ł©ÔÚxÖáÉÏŐÒÒ»”ăPŁŹÊčPA+PB”ÄÖ”ŚîĐĄŁŹČąÇóÂúŚăÌőŒț”Ä”ăP”ÄŚű±êŁ»
Łš3Ł©ÁŹœÓOAŁŹOBŁŹÇóĄśOAB”ÄĂæ»ęŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒËùÊŸ”ÄËÄöÓÊÆ±ÍŒÆŹĐÎŚŽÍêÈ«ÏàÍŹŁŹ·Ö±đÊÇÎÒčúŽúżÆѧŒÒŚæłćÖźĄąÀîʱŐ䥹ŐĆșâĄąÉźÒ»ĐĐŁź°ŃËÄŐĆÍŒÆŹ»ìșÏÔÚÒ»ÆđŁź

Łš1Ł©ÈôËæ»úĂțÈĄÒ»ŐĆÍŒÆŹŁŹÔòĂț”œĄ°ŚæłćÖźĄ±ÍŒÆŹ”ÄžĆÂÊÊÇ__________Ł»
Łš2Ł©ÈôËæ»úĂțÈĄÒ»ŐĆÍŒÆŹÈ»șó·Ć»ŰŁŹÔÙËæ»úĂțÈĄÒ»ŐĆÍŒÆŹŁŹÀûÓĂÁбí»òÊśŚŽÍŒÇóÁœŽÎÖÁÉÙÓĐÒ»ŽÎĂț”œĄ°ŚæłćÖźĄ±ÍŒÆŹ”ÄžĆÂÊŁ»
Łš3Ł©ĐĄ¶«ĄąĐĄÎśĄąĐĄÄÏĄąĐĄ±±ËÄλ͏ѧÒÀŽÎĂțÈĄÍŒÆŹŁŹÈôĐĄ¶«Ăț”œĄ°ŚæłćÖźĄ±ÍŒÆŹŁŹÔòÊŁÏÂÈęÈËÖĐ(ĄĄĄĄĄĄĄĄ)
AŁźĐĄÎśĂț”œĄ°ÀîʱŐäĄ±ÍŒÆŹ”ÄžĆÂÊŽóĄĄĄĄĄĄĄĄBŁźĐĄÄÏĂț”œĄ°ÀîʱŐäĄ±ÍŒÆŹ”ÄžĆÂÊŽó
CŁźĐĄ±±Ăț”œĄ°ÀîʱŐäĄ±ÍŒÆŹ”ÄžĆÂÊŽóĄĄĄĄĄĄĄĄDŁźÈęÈËĂț”œĄ°ÀîʱŐäĄ±ÍŒÆŹ”ÄžĆÂÊÒ»ŃùŽó
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
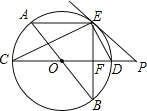
ĄŸÌâÄżĄżÈçÍŒŁŹABĄąCDÎȘĄŃO”ÄÖ±Ÿ¶ŁŹÏÒAEĄÎCDŁŹÁŹœÓBEœ»CDÓÚ”ăFŁŹčę”ăEŚśÖ±ÏßEPÓëCD”ÄŃÓł€Ïßœ»ÓÚ”ăPŁŹÊčĄÏPEDŁœĄÏCŁź
Łš1Ł©ÇóÖ€ŁșPEÊÇĄŃO”ÄÇĐÏߣ»
Łš2Ł©ÇóÖ€ŁșDEÆœ·ÖĄÏBEPŁ»
Łš3Ł©ÈôĄŃO”İ럶ÎȘ10ŁŹCFŁœ2EFŁŹÇóBE”Äł€Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÒ»ŽÎșŻÊęy=kx+bÓë·Ž±ÈÀęșŻÊęy=![]() ”ÄÍŒÏóÏàœÏÓÚAŁš2ŁŹ3Ł©ŁŹBŁš©3ŁŹnŁ©Áœ”㣟
”ÄÍŒÏóÏàœÏÓÚAŁš2ŁŹ3Ł©ŁŹBŁš©3ŁŹnŁ©Áœ”㣟
Łš1Ł©ÇóÒ»ŽÎșŻÊęÓë·Ž±ÈÀęșŻÊę”ÄœâÎöÊœŁ»
Łš2Ł©žùŸĘËùžűÌőŒțŁŹÇëÖ±œÓĐŽłöČ»”ÈÊœkx+bŁŸ![]() ”ÄœâŒŻŁ»
”ÄœâŒŻŁ»
Łš3Ł©čę”ăBŚśBCĄÍxÖᣏŽčŚăÎȘCŁŹÇóSĄśABCŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒ1ŁŹÔÚŸŰĐÎ![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÊÇ
ÊÇ![]() ±ßÉÏÒ»”㣏ÁŹœÓ
±ßÉÏÒ»”㣏ÁŹœÓ![]() ŁŹœ«ŸŰĐÎ
ŁŹœ«ŸŰĐÎ![]() ŃŰ
ŃŰ![]() ŐÛ”țŁŹ¶„”ă
ŐÛ”țŁŹ¶„”ă![]() ÇĄșĂÂäÔÚ
ÇĄșĂÂäÔÚ![]() ±ßÉÏ”ă
±ßÉÏ”ă![]() ŽŠŁŹŃÓł€
ŽŠŁŹŃÓł€![]() œ»
œ»![]() ”ÄŃÓł€ÏßÓÚ”ă
”ÄŃÓł€ÏßÓÚ”ă![]() Łź
Łź
Łš1Ł©ÇóÏ߶Î![]() ”Äł€Ł»
”Äł€Ł»
Łš2Ł©ÈçÍŒ2ŁŹ![]() ŁŹ
ŁŹ![]() ·Ö±đÊÇÏ߶Î
·Ö±đÊÇÏ߶Î![]() ŁŹ
ŁŹ![]() ÉϔĶŻ”㣚Óë¶Ë”ăČ»ÖŰșÏŁ©ŁŹÇÒ
ÉϔĶŻ”㣚Óë¶Ë”ăČ»ÖŰșÏŁ©ŁŹÇÒ![]() Łź
Łź
ąÙÇóÖ€Łș![]() ĄŚ
ĄŚ![]() Ł»
Ł»
ąÚÊÇ·ńŽæÔÚŐâŃù”Ä”ă![]() ŁŹÊč
ŁŹÊč![]() ÊÇ”ÈŃüÈęœÇĐÎŁżÈôŽæÔÚŁŹÇëÇółö
ÊÇ”ÈŃüÈęœÇĐÎŁżÈôŽæÔÚŁŹÇëÇółö![]() ”Äł€Ł»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
”Äł€Ł»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹŐę·œĐÎABCD”Ķ„”ăBÔÚxÖáÉÏŁŹ”ăAĄą”ăCÔÚË«ÇúÏßyŁœ![]() ŁškŁŸ0ŁŹxŁŸ0Ł©ÉÏŁźÈôÖ±ÏßBC”ÄœâÎöÊœÎȘyŁœ
ŁškŁŸ0ŁŹxŁŸ0Ł©ÉÏŁźÈôÖ±ÏßBC”ÄœâÎöÊœÎȘyŁœ![]() x©2ŁŹÔòk”ÄÖ”ÎȘŁšĄĄĄĄŁ©
x©2ŁŹÔòk”ÄÖ”ÎȘŁšĄĄĄĄŁ©
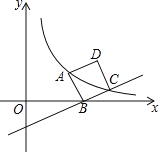
A.24B.12C.6D.4
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
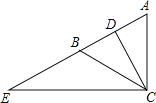
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚĄśABCÖĐŁŹAB=ACŁŹCDÊÇAB±ßÉÏ”ÄÖĐÏߣŹŃÓł€AB”œ”ăEŁŹÊčBE=ABŁŹÁŹœÓCEŁźÇóÖ€ŁșCD= ![]() CEŁź
CEŁź
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com