
【题目】如图,已知AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,AD=2BD,ED与AB的延长线相交于点F,连接AD.
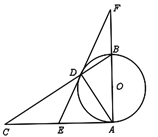
(1)求证:DE为⊙O的切线.
(2)求证:△FDB∽△FAD;
(3)若BF=2,,求⊙O的半径.
【答案】(1)详见解析;(2)详见解析;(3)3
【解析】
(1)连接OD,根据三角形斜边的中线等于斜边的一半可得EA=ED,从而得出∠EDA=∠EAD,通过OD=OA,可得∠EDO=∠EAO,再根据即可推出∠EDO=90°,根据OD为⊙O的半径,即可得证DE为⊙O的切线;
(2)根据DE为⊙O的切线,OD=OB,推算出∠FDB=∠FAD,∠F为公共角,即可证明△FDB∽△FAD;
(3)根据△FDB∽△FAD可得出AF=8,根据![]() 即可求出⊙O的半径.
即可求出⊙O的半径.
(1)证明:连接OD,如图所示:
∵AB为⊙O的直径,
∴∠ADB=∠ADC=90°,
∵E是AC的中点,
∴EA=ED,
∴∠EDA=∠EAD,
∵OD=OA,
∴∠ODA=∠OAD,
∴∠EDO=∠EAO,
∵AB⊥AC,
∴∠EAO=90°,
∴∠EDO=90°,
∵OD为⊙O的半径,
∴DE为⊙O的切线;
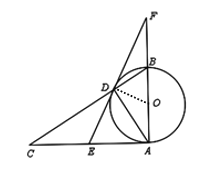
(2)解:∵DE为⊙O的切线,
∴∠ODF=∠FDB+∠ODB=∠FAD+∠OBD=90°,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠FDB=∠FAD,
又∵∠F为公共角,
∴△FDB∽△FAD,
(3)∵△FDB∽△FAD,
∴![]() ,且
,且![]()
∵BF=2
∴![]() =
=![]() .
.
∴DF=4,AF=8.
∴AB=8-2=6.
∴⊙O的半径是3.


科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③a﹣b+c>0;④当x≠1时,a+b>ax2+bx;⑤4ac<b2.其中正确的有( )个
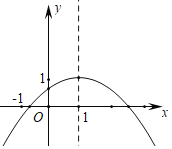
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
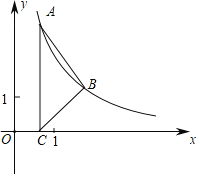
【题目】如图,在平面直角坐标系中,双曲线l:y=![]() (x>0)过点A(a,b),B(2,1)(0<a<2);过点A作AC⊥x轴,垂足为C.
(x>0)过点A(a,b),B(2,1)(0<a<2);过点A作AC⊥x轴,垂足为C.
(1)求l的解析式;
(2)当△ABC的面积为2时,求点A的坐标;
(3)点P为l上一段曲线AB(包括A,B两点)的动点,直线l1:y=mx+1过点P;在(2)的条件下,若y=mx+1具有y随x增大而增大的特点,请直接写出m的取值范围.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进甲、乙两种商品,已知购进甲商品2件和乙商品1件共需50元;购进甲商品1件和乙商品2件共需70元.
(1)求甲、乙两种商品每件的进价分别是多少元?
(2)商场决定甲商品以每件20元出售,乙商品以每件50元出售,为满足市场需求,需购进甲、乙两种商品共60件,且甲种商品的数量不少于乙种商品数量的4倍,请你求出获利最大的进货方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的方格纸中,画出了一个“小老鼠”的图案,已知每个小正方形的边长为1
(1)在上面的方格纸中作出“小老鼠”关于直线DE对称的图案(只画图,不写作法).
(2)以G为原点,GE所在直线为x轴,GH所在直线为y轴,小正方形的边长为单位长度建立直角坐标系,问:是否存在以点Q为顶点,且过点H和E的抛物线,并通过计算说明理由?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )

A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2008年实施国家知识产权战略以来,我国具有独立知识产权的发明专利日益增多.下图显示了2010﹣2013年我国发明专利申请量占世界发明专利申请量的比重.根据统计图提供的信息,下列说法不合理的是( )

A. 统计图显示了2010﹣2013年我国发明专利申请量占世界发明专利申请量的比重的情况
B. 我国发明专利申请量占世界发明专利申请量的比重,由2010年的19.7%上升至2013年的32.1%
C. 2011年我国发明专利申请量占世界发明专利申请量的比重是28%
D. 2010﹣2013年我国发明专利申请量占世界发明专利申请量的比重逐年增长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为
的正方形ABCD与边长为![]() 的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG⊥BE,请你帮他说明理由.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com