
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在第一象限,
在第一象限,![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)cos∠ABO=![]()
【解析】
(1)过点![]() 作
作![]() 点
点![]() ,在
,在![]() 中,利用锐角三角函数的知识求出BD的长,再用勾股定理求出OD、AB、BC的长, 所以AB=BC,从而得到∠ACB=∠BAO,然后根据两角分别相等的两个三角形相似解答即可;
中,利用锐角三角函数的知识求出BD的长,再用勾股定理求出OD、AB、BC的长, 所以AB=BC,从而得到∠ACB=∠BAO,然后根据两角分别相等的两个三角形相似解答即可;
(2)在![]() 中求出∠BAO的余弦值,根据∠ABO=∠BAO可得答案.
中求出∠BAO的余弦值,根据∠ABO=∠BAO可得答案.
(1)在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,
![]() ,
,![]() ,
,
![]() ,∠OAB=∠ABO,
,∠OAB=∠ABO,
过点![]() 作
作![]() 点
点![]() ,
,
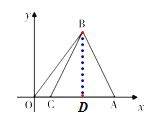
则![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
∴CD=6-2=4,
∴BC=![]() ,
,
∴AB=BC,
∴∠ACB=∠BAO,
∴∠ACB=∠ABO=∠BAO,
又∵∠BAC=∠OAB,
![]() (两角分别相等的两个三角形相似);
(两角分别相等的两个三角形相似);
(2)在![]() 中,
中,
![]() ,
,
∵∠ABO=∠BAO ,
![]() ,
,
即![]() 的值为
的值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,AD=2BD,ED与AB的延长线相交于点F,连接AD.
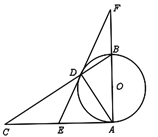
(1)求证:DE为⊙O的切线.
(2)求证:△FDB∽△FAD;
(3)若BF=2,,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
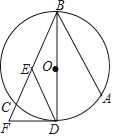
【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,过点D作⊙O的切线交BC的延长线于点F.
(1)求证:EF=ED;
(2)如果半径为5,cos∠ABC=![]() ,求DF的长.
,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
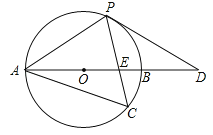
【题目】如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.
(1)试判断PD与⊙O的位置关系,并说明理由;
(2)若点C是弧AB的中点,已知AB=4,求CECP的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为∠MBN角平分线上一点,⊙O与BN相切于点C,连结CO并延长交BM于点A,过点A作AD⊥BO于点D.
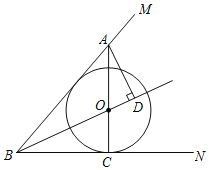
(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的小正方形网格中,勤奋学习小组的同学画出了五边形
的小正方形网格中,勤奋学习小组的同学画出了五边形![]() 和五边形
和五边形![]() 则下列说法中,不正确的是( )
则下列说法中,不正确的是( )

A.五边形![]()
![]() 五边形
五边形![]()
B.![]()
C.五边形![]() 的周长是五边形
的周长是五边形![]() 周长的
周长的![]() 倍.
倍.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,某矩形游泳池ABCD,BC长为25m,小林和小明分别在游泳池的AB、CD两边,同时沿各自的泳道朝另一边游泳,设他们游泳的时间为t(s),离AB边的距离为y(m),图②中的实线和虚线分别是小明和小林在游泳过程中y与t的函数图象(0≤t≤180).下面的四个结论:
①小明游泳的平均速度小于小林游泳的平均速度;
②小明游泳的路程大于小林游泳的路程;
③小明游75m时,小林游了90m;
④小明与小林共相遇5次.
其中所有正确结论的序号是( )
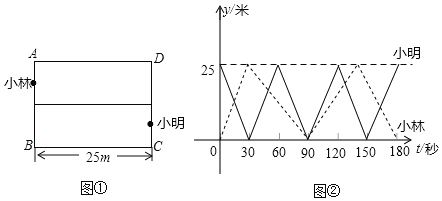
A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 内接于
内接于![]() ,对角线
,对角线![]() 为
为![]() 的直径,过点
的直径,过点![]() 作
作![]() 的垂线交
的垂线交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 于点
于点![]() .
.
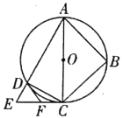
(1)求证:![]() ;
;
(2)填空:
①当![]() 的度数为 时,四边形
的度数为 时,四边形![]() 为正方形;
为正方形;
②若![]() ,
,![]() ,则四边形
,则四边形![]() 的最大面积是 .
的最大面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,AB是⊙O的直径,点P在AB的延长线上,弦CE交AB于点,连结OE,AC,且∠P=∠E,∠POE=2∠CAB.
(1)求证:CE⊥AB;
(2)求证:PC是⊙O的切线;
(3)若BD=2OD,且PB=9,求⊙O的半径长和tan∠P的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com