
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则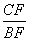 的值为( )
的值为( )

A.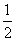 B.
B.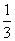 C.
C.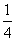 D.
D.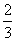
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论: ①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
C.
【解析】A.如图,反比例函数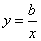 经过第一、三象限,则b>0.所以a<0.则一次函数
经过第一、三象限,则b>0.所以a<0.则一次函数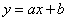 的图象应该经过第一、二、四象限.故本选项错误;
的图象应该经过第一、二、四象限.故本选项错误;
B.如图,反比例函数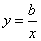 经过第二、四象限,则b<0.所以a>0.则一次函数
经过第二、四象限,则b<0.所以a>0.则一次函数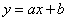 的图象应该经过第一、二、三象限.故本选项错误;
的图象应该经过第一、二、三象限.故本选项错误;
C.如图,反比例函数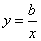 经过第一、三象限,则b>0.所以a<0.则一次函数
经过第一、三象限,则b>0.所以a<0.则一次函数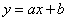 的图象应该经过第一、二、四象限.故本选项正确;
的图象应该经过第一、二、四象限.故本选项正确;
D.如图,反比例函数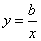 经过第二、四象限,则b<0.所以a>0.则一次函数
经过第二、四象限,则b<0.所以a>0.则一次函数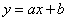 的图象应该经过第一、二、四象限.故本选项错误;
的图象应该经过第一、二、四象限.故本选项错误;
故选C.
查看答案和解析>>
科目:初中数学 来源: 题型:
C
【解析】因为AB=AC,∠A=50°,所以∠B=∠C=65°,又因为BD=CE,BE=CF,所以ΔBDE≌ΔCEF,所 以∠BED=∠CFE,因为∠CFE+∠CEF=180°-65°=115°,所以∠BED+∠CEF=115°,所以∠DEF=180°-(∠BED+∠CEF)=180°-115°=65°,
以∠BED=∠CFE,因为∠CFE+∠CEF=180°-65°=115°,所以∠BED+∠CEF=115°,所以∠DEF=180°-(∠BED+∠CEF)=180°-115°=65°,
故选C.
查看答案和解析>>
科目:初中数学 来源: 题型:
C.
【解析】如果将图①看作是铺成的一个1×1的正方形图案,图②看作是铺成的一个2×2的正方形图案,图③看作是铺成的一个3×3的正方形图案,图④看作是铺成的一个4×4的正方形图案,那么根据给出的四个图形的规律可以知道,组成大正方形的每个小正方形上有一个完整的圆,因此圆的数目是大正方形边长的平方;又每四个小正方形组成一个完整的圆,这样的圆的个数是大正方形的边长减1的平方,从而可得第10个图中完整的圆共有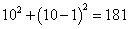 个.
个.
故选C.
查看答案和解析>>
科目:初中数学 来源: 题型:
铜陵学院毕业生小张响应国家“自主创业”的号召,投资开办了一个装饰品商店,该店采购进一种今年新上市的饰品进行了30天的试销售,购进价格为20元/件.销售结束后,得知日销售量P(件)与销售时间x(天)之间有如下关系: (1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系:
(1≤x≤30,且x为整数);又知前20天的销售价格Q1(元/件)与销售时间x(天)之间有如下关系: (1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1≤x≤20,且x为整数),后10天的销售价格Q2(元/件)与销售时间x(天)之间有如下关系:Q2=45(21≤x≤30,且x为整数).
(1)第25天该商店的日销售利润为多少元?
(2)试写出该商店日销售利润y(元)关于销售时间x(天)之间的函数关系式;
(2)请问在这30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h(休息前后的速度一致),如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则当乙车行驶 小时后,两车恰好相距50km.
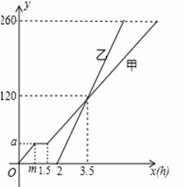
查看答案和解析>>
科目:初中数学 来源: 题型:
“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售量较好的肉馅粽、豆沙粽、红枣粽、蛋黄馅粽(以下分别用A、B、C、D表示这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查结果绘制成如下两幅统计图.
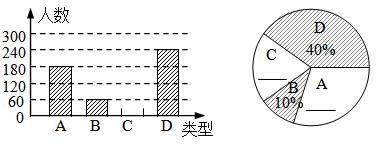
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将不完整的条形图补充完整.
(3)若居民区有8000人,请估计爱吃D粽的人数?
(4)若有外型完全相同的A、B、C、D粽各一个煮熟后,小王吃了俩个,用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com