
【题目】如图,在锐角![]() 中,
中,![]() 是
是![]() 边上的高.
边上的高. ![]() ,且
,且![]()
![]() .连接
.连接![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中一定正确的个数是( )
.其中一定正确的个数是( )

A.![]() 个B.
个B.![]() 个
个
C.![]() 个D.
个D.![]() 个
个
【答案】A
【解析】
首先根据题意,可得出∠FAE+∠BAD=90°,∠GAE+∠CAD=90°,进而得出∠FAE+∠BAD+∠GAE+∠CAD=180°,可判定①结论正确;由∠BAF+∠BAC=∠CAG+∠BAC,![]() ,得出∠FAC=∠BAG,
,得出∠FAC=∠BAG,![]()
![]() ,判定△FAC≌△BAG,判定②结论正确;由∠EAF+∠BAD=90°,∠BAD+∠ABC=90°,得出∠EAF=∠ABC,可判定④结论正确;由∠AFC=∠ABG,∠AFC+∠FHA=90°,对顶角相等,得出∠ABG+∠BHC=90°,即可判定③结论正确;故正确的结论有4个.
,判定△FAC≌△BAG,判定②结论正确;由∠EAF+∠BAD=90°,∠BAD+∠ABC=90°,得出∠EAF=∠ABC,可判定④结论正确;由∠AFC=∠ABG,∠AFC+∠FHA=90°,对顶角相等,得出∠ABG+∠BHC=90°,即可判定③结论正确;故正确的结论有4个.
解:∵![]() 是
是![]() 边上的高.
边上的高. ![]() ,
,
∴∠FAE+∠BAD=90°,∠GAE+∠CAD=90°
∴∠FAE+∠BAD+∠GAE+∠CAD=180°
∴![]() ,①结论正确;
,①结论正确;
∵![]()
∴∠BAF+∠BAC=∠CAG+∠BAC
∴∠FAC=∠BAG
又∵![]()
![]()
∴△FAC≌△BAG(SAS)
∴BG=CF,②结论正确;
∵∠EAF+∠BAD=90°,∠BAD+∠ABC=90°
∴∠EAF=∠ABC,④结论正确;
令CF和AB、BG分别交于点H、I
∵△FAC≌△BAG
∴∠AFC=∠ABG
又∵∠AFC+∠FHA=90°,∠FHA=∠BHC(对顶角相等)
∴∠ABG+∠BHC=90°,即∠BIF=90°,即![]() ,
,
③结论正确;正确的个数有4个.
故选:A.



 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,但始终保持EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF;
(2)若正方形的边长为4,设AE=x,BF=y,求y与x之间的函数解析式;
(3)当x取何值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
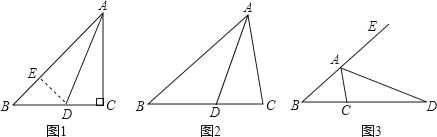
【题目】在△ABC中,∠ACB=2∠B,如图①,当∠C=90°,AD为∠BAC的角平分线时,在AB上截取AE=AC,连接DE,易证AB=AC+CD.
(1)如图②,当∠C≠90°,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想:
(2)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
合计 | ________ | 1 |

根据上述信息,解答下列问题:
(1)这次书法作品比赛成绩的调查是采用_____(填“普查”或“抽样调查”),样本是_____.
(2)完成上表,并补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级奖的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
(1)当t为何值时,四边形PODB是平行四边形?
(2)△OPD为等腰三角形时,写出点P的坐标(请直接写出答案,不必写过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,![]() ,
,![]() 分别在直线
分别在直线![]() 上,
上,![]() 是平面内一点,
是平面内一点,![]() 和
和![]() 的平分线所在直线相交于点
的平分线所在直线相交于点![]() .
.
(1)如图1,当![]() 都在直线
都在直线![]() 之间,且
之间,且![]() 时,
时,![]() 的度数为_________;
的度数为_________;
(2)如图2,当![]() 都在直线
都在直线![]() 上方时,探究
上方时,探究![]() 和
和![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
(3)如图3,当![]() 在直线
在直线![]() 两侧时,直接写出
两侧时,直接写出![]() 和
和![]() 之间的数量关系是_____.
之间的数量关系是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:数学课上,老师展示了一位同学的作业如下:
已知多项式![]() ,
,![]() ,
,![]()
(1)求![]() ;
;
(2)若![]() 的结果与字母
的结果与字母![]() 的取值无关,求
的取值无关,求![]() 的值.
的值.
下面是这位同学第(1)问的解题过程:
解:(1)![]() …………………………第一步
…………………………第一步
![]() …………………………………………………第二步
…………………………………………………第二步
![]() ……………………………………………………………第三步
……………………………………………………………第三步
回答问题:
(i)这位同学第______步开始出现错误,错误原因是____________;
(ii)请你帮这位同学完成题目中的第(2)问.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com