
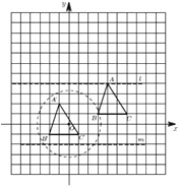
【题目】正方形网格中,每个小正方形的边长为1个单位长度建立如图所示的平面直角坐标系,![]() 的顶点均为格点,把
的顶点均为格点,把![]() 向左平移5个单位长度,再向下平移2个单位长度,得到
向左平移5个单位长度,再向下平移2个单位长度,得到![]() .
.

(1)在图中画出![]() ;
;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() 与
与![]() 的面积相等,则点
的面积相等,则点![]() 的坐标为 ;
的坐标为 ;
(3)横、纵坐标均为整数的点称为整数点,在第一象限中的整数点![]() 满足
满足![]() ,直接写出整数点
,直接写出整数点![]() 的所有可能坐标.
的所有可能坐标.
【答案】(1)画图见解析
(2)![]() ;
;![]()
(3)![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)把![]() 每个顶点向左平移5个单位长度,再向下平移2个单位长度,连接平移后的三个顶点,即可得到
每个顶点向左平移5个单位长度,再向下平移2个单位长度,连接平移后的三个顶点,即可得到![]() .
.
(2)![]() 与
与![]() 的面积相等,且它们由公共的底边
的面积相等,且它们由公共的底边![]() ,点P到BC边的距离为3,且点
,点P到BC边的距离为3,且点![]() 在
在![]() 轴上,即可求得点P的坐标.
轴上,即可求得点P的坐标.
(3)采用作图的方式,点![]() 在以
在以![]() 为圆心、
为圆心、![]() 为直径的圆内,又点
为直径的圆内,又点![]() 在第一象限,即可确定M符合条件的点.
在第一象限,即可确定M符合条件的点.
(1)如图所示,![]() 即为所求:
即为所求:

(2)![]() 与
与![]() 的面积相等,且它们由公共的底边
的面积相等,且它们由公共的底边![]() ,
,
∴两三角形在![]() 边上的高相等
边上的高相等
即点P到BC边的距离为3,
又∵点![]() 在
在![]() 轴上,
轴上,
可得点P的坐标为![]() 或
或![]() ,
,
故答案为:![]() 或
或![]() .
.
(3)如图,点![]() 在以
在以![]() 为圆心、
为圆心、![]() 为直径的圆内,又点
为直径的圆内,又点![]() 在第一象限,所以点
在第一象限,所以点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
,![]() .
.
故答案为:![]() ,
,![]() ,
,![]() ,
,![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了![]() (n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应
(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应![]() 展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中的系数等等.
展开式中的系数等等.

(1)根据上面的规律,写出![]() 的展开式.
的展开式.
(2)利用上面的规律计算:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .将点
.将点![]() 向右平移
向右平移![]() 个单位长度得到点
个单位长度得到点![]() ,如图所示.
,如图所示.

(1)求点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,沿着线段
出发,沿着线段![]() 、线段
、线段![]() 以
以![]() 个单位长度/秒的速度运动,同时点
个单位长度/秒的速度运动,同时点![]() 从点
从点![]() 出发沿着线段
出发沿着线段![]() 以
以![]() 个单位长度秒的速度运动,设运动时间为
个单位长度秒的速度运动,设运动时间为![]() 秒
秒![]() .当
.当![]() 时,求
时,求![]() 的取值范围;是否存在一段时间,使得
的取值范围;是否存在一段时间,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC为直角,以AB为直径作⊙O交AC于点D,点E为BC中点,连结DE,DB
(1)求证:DE与⊙O相切;
(2)若∠C=30°,求∠BOD的度数;
(3)在(2)的条件下,若⊙O半径为2,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AC,BD交于点O,折叠正方形ABCD,使AB边落在AC上,点B落在点H处,折痕AE分别交BC于点E,交BO于点F,连结FH,则下列结论正确的有几个( )
⑴AD=DF;(2) ![]() =
= ![]() ;(3)
;(3) ![]() =
= ![]() ﹣1;(4)四边形BEHF为菱形.
﹣1;(4)四边形BEHF为菱形.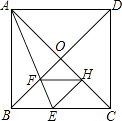
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]()
(1)请按下列要求画图:
①将![]() 先向右平移
先向右平移![]() 个单位长度、再向上平移
个单位长度、再向上平移![]() 个单位长度,得到
个单位长度,得到![]() ,画出
,画出![]()
②![]() 与
与![]() 关于原点
关于原点![]() 成中心对称,画出
成中心对称,画出![]()
③画出![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得到的
后得到的![]()
(2)在![]() 中所得的
中所得的![]() 和
和![]() 关于点
关于点![]() 成中心对称,请直接写出对称中心
成中心对称,请直接写出对称中心![]() 点的坐标.
点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物流公司承接A,B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.
(1)该物流公司月运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com