Question

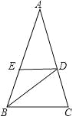
【题目】如图，Rt△ABC中，∠ABC为直角，以AB为直径作⊙O交AC于点D，点E为BC中点，连结DE，DB

（1）求证：DE与⊙O相切；
（2）若∠C=30°，求∠BOD的度数；
（3）在（2）的条件下，若⊙O半径为2，求阴影部分面积．

Answer 1

【答案】
（1）证明：连结OD，

∵AB为⊙O为直径，

∴∠ADB=∠BDC=90°，

又∵E是斜边BC的中点

∴DE=BE=CE，

∴∠BDE=∠DBE，

∵OD=OB，

∴∠ODB=∠OBD

∴∠ODE=∠ODB+∠BDE=∠OBD+∠DBE=∠ABC=90°

即DE与⊙O相切．

（也可以通过证明△OBE≌△ODE得到∠ODE=∠OBE=90°）

（2）解：若∠C=30°而DE=CE，

∴∠DEB=60°

在四边形OBED中，则∠BOD=360°﹣90°﹣90°﹣60°=120°

（3）解：连结OE，则∠OED=∠OEB=30°

∵OD=OB=2∴DE=BE=2

∴S阴影部分=S四边形OBED﹣S扇形OBD=S△OBE+S△ODE﹣S扇形OBD

=2 +2 ﹣ =4 ﹣ ．

【解析】（1）要证明DE与与⊙O相切；只要证明∠ODE=∠ODB+∠BDE=∠OBD+∠DBE=∠ABC=90°即可；（2）在四边形OBED中，利用四边形的内角和求∠BOD即可；（3）用S阴影部分=S四边形OBED﹣S扇形OBD=S△OBE+S△ODE﹣S扇形OBD计算即可。
【考点精析】解答此题的关键在于理解切线的判定定理的相关知识，掌握切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线，以及对扇形面积计算公式的理解，了解在圆上，由两条半径和一段弧围成的图形叫做扇形；扇形面积S=π（R2-r2）．