
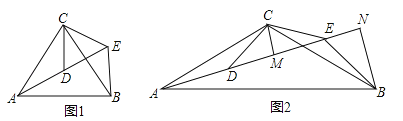
【题目】如图,△ACB和△DCE均为等腰三角形,点A,D,E在同一直线上,连接BE.
(1)如图1,若∠CAB=∠CBA=∠CDE=∠CED=50°
①求证:AD=BE;
②求∠AEB的度数.
(2)如图2,若∠ACB=∠DCE=120°,CM为△DCE中DE边上的高,BN为△ABE中AE边上的高,试证明:AE=![]() CM+
CM+![]() BN.
BN.
【答案】(1)①证明见解析;②80°;(2)证明见解析.
【解析】
试题分析:(1)①通过角的计算找出∠ACD=∠BCE,再结合△ACB和△DCE均为等腰三角形可得出“AC=BC,DC=EC”,利用全等三角形的判定(SAS)即可证出△ACD≌△BCE,由此即可得出结论AD=BE;
②结合①中的△ACD≌△BCE可得出∠ADC=∠BEC,再通过角的计算即可算出∠AEB的度数;
(2)根据等腰三角形的性质结合顶角的度数,即可得出底角的度数,利用(1)的结论,通过解直角三角形即可求出线段AD、DE的长度,二者相加即可证出结论.
试题解析:(1)①证明:∵∠CAB=∠CBA=∠CDE=∠CED=50°,∴∠ACB=∠DCE=180°﹣2×50°=80°.
∵∠ACB=∠ACD+∠DCB,∠DCE=∠DCB+∠BCE,∴∠ACD=∠BCE.
∵△ACB和△DCE均为等腰三角形,∴AC=BC,DC=EC.
在△ACD和△BCE中,∵AC=BC,∠ACD=∠BCE,DC=EC,∴△ACD≌△BCE(SAS),∴AD=BE.
②解:∵△ACD≌△BCE,∴∠ADC=∠BEC.
∵点A,D,E在同一直线上,且∠CDE=50°,∴∠ADC=180°﹣∠CDE=130°,∴∠BEC=130°.
∵∠BEC=∠CED+∠AEB,且∠CED=50°,∴∠AEB=∠BEC﹣∠CED=130°﹣50°=80°.
(2)证明:∵△ACB和△DCE均为等腰三角形,且∠ACB=∠DCE=120°,∴∠CDM=∠CEM=![]() ×(180°﹣120°)=30°.
×(180°﹣120°)=30°.
∵CM⊥DE,∴∠CMD=90°,DM=EM.
在Rt△CMD中,∠CMD=90°,∠CDM=30°,∴DE=2DM=2×![]() =
=![]() CM.
CM.
∵∠BEC=∠ADC=180°﹣30°=150°,∠BEC=∠CEM+∠AEB,∴∠AEB=∠BEC﹣∠CEM=150°﹣30°=120°,∴∠BEN=180°﹣120°=60°.
在Rt△BNE中,∠BNE=90°,∠BEN=60°,∴BE=![]() =
=![]() BN.
BN.
∵AD=BE,AE=AD+DE,∴AE=BE+DE=![]() CM+
CM+![]() BN.
BN.


科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
在某场CBA比赛中,某位运动员的技术统计如下表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 (次) | 罚球得分(分) | 篮板 (个) | 助攻(次) | 个人总得分(分) |
数据 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:(1)表中出手投篮次数和投中次数均不包括罚球;
(2)总得分=两分球得分+三分球得分+罚球得分.
根据以上信息,求本场比赛中该运动员投中两分球和三分球各几个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AB∥OC,BC∥AO,A、C两点的坐标分别为(﹣ ![]() ,
, ![]() )、(﹣2
)、(﹣2 ![]() ,0),A、B两点间的距离等于O、C两点间的距离.
,0),A、B两点间的距离等于O、C两点间的距离.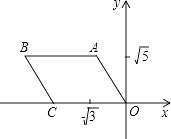
(1)点B的坐标为;
(2)将这个四边形向下平移2 ![]() 个单位长度后得到四边形A′B′C′O′,请你写出平移后四边形四个顶点的坐标.
个单位长度后得到四边形A′B′C′O′,请你写出平移后四边形四个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,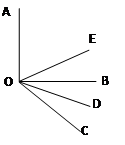
(1)如果∠AOB=90°,∠BOC=40°,求∠DOE的度数;
(2)如果∠AOB= ![]() ,∠BOC=
,∠BOC= ![]() (
( ![]() 、
、 ![]() 均为锐角,
均为锐角, ![]() >
> ![]() ),其他条件不变,求∠DOE;
),其他条件不变,求∠DOE;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com