
【题目】东坡商贸公司购进某种水果的成本为20元/kg,经市场调研发现,这种水果在未来48天的销售价格p(元/kg)与时间t(天)之间的函数关系式为p=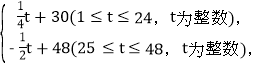 且日销售量y(kg)与销售时间t(天)的关系如下表:
且日销售量y(kg)与销售时间t(天)的关系如下表:

(1)已知y与t的变化规律符合一次函数关系,试求在第30天的日销售量是多少;
(2)问哪一天的销售利润最大,最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
【答案】(1)第30天的日销售量为60千克;(2)在第10天的销售利润最大,最大日销售利润为1 250元;(3)7≤n<9.
【解析】分析:(1)设y=kt+b,利用待定系数法即可解决问题.
(2)日利润=日销售量×每公斤利润,据此分别表示前24天和后24天的日利润,根据函数性质求最大值后比较得结论.
(3)列式表示前24天中每天扣除捐赠后的日销售利润,根据函数性质求n的取值范围.
详解:(1)设y=kt+b,把t=1,y=118;t=3,y=114代入得到:
![]() 解得
解得![]() ,
,
∴y=120-2t,
当t=30时,y=120-60=60.
即在第30天的日销售量为60千克.
(2)设日销售利润为w元,则w=(p-20)y.
当1≤t≤24时,w=![]() (120-2t)=-
(120-2t)=-![]() t2+10t+1 200=-
t2+10t+1 200=-![]() (t-10)2+1 250.
(t-10)2+1 250.
∴当t=10时,w最大=1 250.
当25≤t≤48时,w=![]() (120-2t)=t2-116t+3 360=(t-58)2-4,
(120-2t)=t2-116t+3 360=(t-58)2-4,
由二次函数的图象及性质知当t=25时,w最大=1 085.
∵1 250>1 085,
∴在第10天的销售利润最大,最大日销售利润为1 250元.
(3)设每天扣除捐赠后的日销售利润为w1元,
依题意得w1=![]() (120-2t).
(120-2t).
=-![]() t2+2(n+5)t+1 200-120n(1≤t≤24),
t2+2(n+5)t+1 200-120n(1≤t≤24),
其图象的对称轴为直线t=2n+10,
要使w1随t的增大而增大,
由二次函数的图象及性质知2n+10≥24,解得n≥7.
又∵n<9,∴7≤n<9.


科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,点
,点![]() 是
是![]() 、
、![]() 之间(不在直线
之间(不在直线![]() ,
,![]() 上)的一个动点,
上)的一个动点,
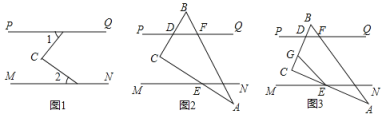
(1)若![]() 与
与![]() 都是锐角,如图1,请直接写出
都是锐角,如图1,请直接写出![]() 与
与![]() ,
,![]() 之间的数量关系;
之间的数量关系;
(2)若把一块三角尺(![]() ,
,![]() )按如图2方式放置,点
)按如图2方式放置,点![]() ,
,![]() ,
,![]() 是三角尺的边与平行线的交点,若
是三角尺的边与平行线的交点,若![]() ,求
,求![]() 的度数;
的度数;
(3)将图乙中的三角尺进行适当转动,如图3,直角顶点![]() 始终在两条平行线之间,点
始终在两条平行线之间,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,且有
,且有![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数![]() 在数轴上对应的点分别为
在数轴上对应的点分别为![]() ,其中b是最小的正整数,
,其中b是最小的正整数,![]() 满足
满足![]() .
.
(1)填空:![]() __________,
__________,![]() _____________,
_____________,![]() ___________;
___________;
(2)现将点A,点B和点C分别以每秒4个单位长度,1个单位长度和1个单位长度的速度在数轴上同时向右运动,设运动时间为t秒.
i)定义:已知![]() 为数轴上任意两点,将数轴沿线段
为数轴上任意两点,将数轴沿线段![]() 的中点Q进行折叠,点M与点N刚好重合,所以我们又称线段
的中点Q进行折叠,点M与点N刚好重合,所以我们又称线段![]() 的中点Q为点M和点N的折点.
的中点Q为点M和点N的折点.
试问:当t为何值时,这三个点中恰好有一点为另外两点的折点?
ii)当点A在点C左侧时(不考虑点A与点B重合),是否存在一个常数m,使得![]() 的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.
的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去……
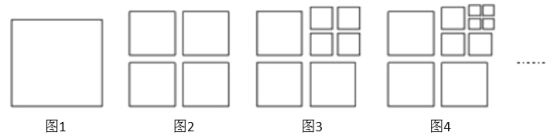
(1)根据图中的规律补全下表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
| n |
正方形个数 | 1 | 4 | 7 | 10 |
|
(2)求第几幅图形中有2020个正方形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】多边形上或内部的一点与多边形各顶点的连线,可以将多边形分割成若干个小三角形.如图,给出了四边形的三种具体分割方法,分别将四边形分割成了2个、3个、4个小三角形,这样我们就可以借助研究三角形的经验研究四边形了.
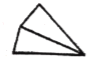
图①被分割成2个小三角形

图②被分割成3个小三角形

图③被分割成4个小三角形
(1)请按照上述三种方法分别将图中的六边形进行分割,并写出每种方法所得到的小三角形的个数:
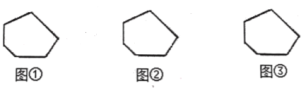
图①被分割成 个小三角形、图②被分割成 个小三角形、图③被分割成 个小三角形;
(2)如果按照上述三种分割方法分别分割![]() 边形,请写出每种方法所得到的小三角形的个数(用含
边形,请写出每种方法所得到的小三角形的个数(用含![]() 的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,
的代数式写出结论即可,不必画图):按照上述图①、图②、图③的分割方法,![]() 边形分别可以被分割成 、 、 个小三角形.
边形分别可以被分割成 、 、 个小三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com