
【题目】已知有理数![]() 在数轴上对应的点分别为
在数轴上对应的点分别为![]() ,其中b是最小的正整数,
,其中b是最小的正整数,![]() 满足
满足![]() .
.
(1)填空:![]() __________,
__________,![]() _____________,
_____________,![]() ___________;
___________;
(2)现将点A,点B和点C分别以每秒4个单位长度,1个单位长度和1个单位长度的速度在数轴上同时向右运动,设运动时间为t秒.
i)定义:已知![]() 为数轴上任意两点,将数轴沿线段
为数轴上任意两点,将数轴沿线段![]() 的中点Q进行折叠,点M与点N刚好重合,所以我们又称线段
的中点Q进行折叠,点M与点N刚好重合,所以我们又称线段![]() 的中点Q为点M和点N的折点.
的中点Q为点M和点N的折点.
试问:当t为何值时,这三个点中恰好有一点为另外两点的折点?
ii)当点A在点C左侧时(不考虑点A与点B重合),是否存在一个常数m,使得![]() 的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.
的值在一定时间范围内不随t的改变而改变?若存在,求出m的值;若不存在,请说明理由.
【答案】(1)-2,1,5;(2)i)当t= ![]() 或t=
或t=![]() 时,这三个点中恰好有一点为另外两点的折点;ii)存在,当常数m=2时,
时,这三个点中恰好有一点为另外两点的折点;ii)存在,当常数m=2时,![]() 的值在一定时间范围内不随t的改变而改变.
的值在一定时间范围内不随t的改变而改变.
【解析】
(1)根据b是最小的正整数得到b=1,根据![]() 求出a=-2,c=5;
求出a=-2,c=5;
(2)i)先得到运动t秒后三个点对应的数,再分三种情况分别计算t的值;
ii)先分别用t表示出AC、AB,再根据![]() 将AC、AB的式子代入即可求出常数m的值.
将AC、AB的式子代入即可求出常数m的值.
(1)∵b是最小的正整数,
∴b=1,
∵![]() ,
,
∴a+2=0,c-5=0,
∴a=-2,c=5,
故答案为:-2,1,5;
(2)
i)t秒后点A、B、C表示的数分别是:4t-2,1+t,5+t,
当点A是中点时,1+t+5+t=2(4t-2),得t= ![]() ,
,
当点B是中点时,4t-2+5+t=2(1+t),得t=![]() (舍去),
(舍去),
当点C是中点时,4t-2+1+t=2(5+t),得t=![]() ,
,
综上,当t= ![]() 或t=
或t=![]() 时,这三个点中恰好有一点为另外两点的折点;
时,这三个点中恰好有一点为另外两点的折点;
ii)存在,
∵t秒后点A、B、C表示的数分别是:4t-2,1+t,5+t,
∴AC=5+t-4t+2=7-3t,
当点A在点B的右侧时即AB =4t-2-1-t =3t-3时,
![]() =
= ![]() ,
,
∴常数m=2,此时![]() =2AC+2AB=8,即AC+AB=4,
=2AC+2AB=8,即AC+AB=4,
∵AC+AB=7-3t+3t-3=4,
∴当常数m=2时,![]() 的值在一定时间范围内不随t的改变而改变;
的值在一定时间范围内不随t的改变而改变;
当点B在点A右侧即AB=1+t-4t+2=3-3t时,
![]() =
=![]() ,
,
∴常数m=-2,此时![]() =2AC-2AB=20,即AC-AB=10,
=2AC-2AB=20,即AC-AB=10,
∵7-3t-(3-3t)=4,
∴m=-2舍去,
综上,当常数m=2时,![]() 的值在一定时间范围内不随t的改变而改变.
的值在一定时间范围内不随t的改变而改变.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
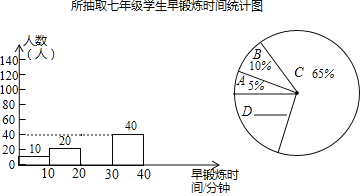
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市元月1日搞促销活动,购物不超过200元不给优惠;超过200元,而不超过500元优惠10%,超过500元的,其中500元按9折优惠,超过的部分按8折优惠,某人两次购物分别用了134元、466元.
(1)此人两次购物时物品不打折分别值多少钱?
(2)在这次活动中他节省了多少钱?
(3)若此人将两次购买的物品合起来一次购买是不是更合算?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年底,我国高铁总运营里程达3.5万公里,居世界第一.已知![]() 两市之间开通了“复兴号”与“和谐号”高铁列车.某日“和谐号”列车以每小时200km的速度匀速从A市驶向B市,1小时后“复兴号”列车以每小时300km的速度也匀速从A市驶向B市.
两市之间开通了“复兴号”与“和谐号”高铁列车.某日“和谐号”列车以每小时200km的速度匀速从A市驶向B市,1小时后“复兴号”列车以每小时300km的速度也匀速从A市驶向B市.
(1)试问:“复兴号”列车出发多少小时后,两列车的车头相距50km;
(2)若“复兴号”与“和谐号”列车的车长都为200m,从“复兴号”列车的车头追上“和谐号”列车的车尾开始计时,直到“复兴号”列车刚好完全超过“和谐号”列车为止,共持续了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活质量的提高,观光旅游已经成为人们休闲度假的一种方式.对于假期的安排,旅游部门随机电话访谈若干名市民,调查了解他们假期间选择外出游玩的类型:近郊游、国内长线游、出国游和其他.根据电话访谈的结果制成统计图,根据没有制作完成的统计图提供的信息回答下列问题.
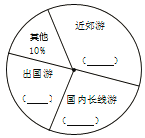
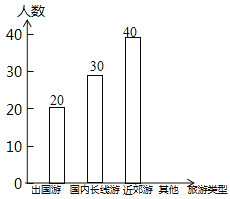
(1)选择其他方式的人数是多少?
(2)补全条形统计图和扇形统计图;
(3)若A,B在 4月3号在①“西岭雪山”、②安仁古镇和③新场古镇三个地方中选择其中的一地方游玩.(三个景点被A和B选中的可能性相同).用树状图或者列表法写出A,B两人选择的所有可能结果,并求A,B两人选择在不同地方游玩的概率.(树状图或者列表可以直接用每个景点前的数字番号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东坡商贸公司购进某种水果的成本为20元/kg,经市场调研发现,这种水果在未来48天的销售价格p(元/kg)与时间t(天)之间的函数关系式为p=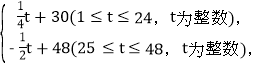 且日销售量y(kg)与销售时间t(天)的关系如下表:
且日销售量y(kg)与销售时间t(天)的关系如下表:

(1)已知y与t的变化规律符合一次函数关系,试求在第30天的日销售量是多少;
(2)问哪一天的销售利润最大,最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象,现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的ALMN,若中间空白部分四边形OPQR恰好是正方形,且ALMN的面积为50,则正方形EFGH的面积为( )
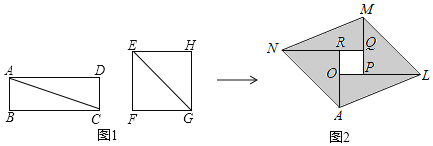
A. 24 B. 25 C. 26 D. 27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com