
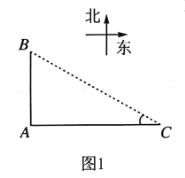
【题目】如图1,![]() 是聊城市开发区三个垃圾存放点,点
是聊城市开发区三个垃圾存放点,点![]() 分别位于点
分别位于点![]() 的正北和正东方向,
的正北和正东方向, ![]() 米.八位环卫工人分别测得的
米.八位环卫工人分别测得的![]() 长度如下表:
长度如下表:
甲 | 乙 | 丙 | 丁 | 戊 | 戌 | 申 | 辰 | |
|
|
|
|
|
|
|
|
|
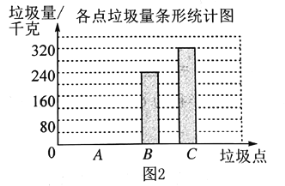
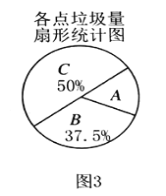
他们又调查了各点的垃圾量,并绘制了下列尚不完整的统计图2、图3.
![]() 求表中
求表中![]() 长度的平均数
长度的平均数![]() ;
;
![]() 求
求![]() 处的垃圾量,并将图2补充完整;
处的垃圾量,并将图2补充完整;
![]() 用(1)中的
用(1)中的![]() 作为
作为![]() 的长度,要将
的长度,要将![]() 处的垃圾沿道路
处的垃圾沿道路![]() 都运到
都运到![]() 处,已知运送
处,已知运送![]() 千克垃圾每米的费用为
千克垃圾每米的费用为![]() 元,求运垃圾所需的费用(结果保留根号).
元,求运垃圾所需的费用(结果保留根号).
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知函数y= (n为常数).
(n为常数).
(1)当n=1时,
①点P(﹣3,m)在此函数图象上,求m的值.
②当﹣4≤x≤3时,求此函数的最大值和最小值.
(2)当x<n时,若此函数的图象与坐标轴只有两个交点,求n的取值范围.
(3)若n>0,当此函数的图象与以A(0,3)、B(5,﹣2)、C(﹣5,﹣2)、D(﹣5,3)为顶点的四边形的边有且只有四个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
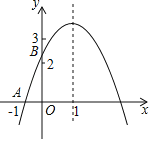
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),下列结论:
①当﹣1<x<3时,y>0;②﹣1<a<﹣![]() ;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂制作![]() 两种手工艺品,
两种手工艺品,![]() 每天每件获利比
每天每件获利比![]() 多105元,获利30元的
多105元,获利30元的![]() 与获利240元的
与获利240元的![]() 数量相等.
数量相等.
(1)制作一件![]() 和一件
和一件![]() 分别获利多少元?
分别获利多少元?
(2)工厂安排65人制作![]() ,
,![]() 两种手工艺品,每人每天制作2件
两种手工艺品,每人每天制作2件![]() 或1件
或1件![]() .现在在不增加工人的情况下,增加制作
.现在在不增加工人的情况下,增加制作![]() .已知每人每天可制作1件
.已知每人每天可制作1件![]() (每人每天只能制作一种手工艺品),要求每天制作
(每人每天只能制作一种手工艺品),要求每天制作![]() ,
,![]() 两种手工艺品的数量相等.设每天安排
两种手工艺品的数量相等.设每天安排![]() 人制作
人制作![]() ,
,![]() 人制作
人制作![]() ,写出
,写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)在(1)(2)的条件下,每天制作![]() 不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知
不少于5件.当每天制作5件时,每件获利不变.若每增加1件,则当天平均每件获利减少2元.已知![]() 每件获利30元,求每天制作三种手工艺品可获得的总利润
每件获利30元,求每天制作三种手工艺品可获得的总利润![]() (元)的最大值及相应
(元)的最大值及相应![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交点C,抛物线
与x轴交于点A,与y轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
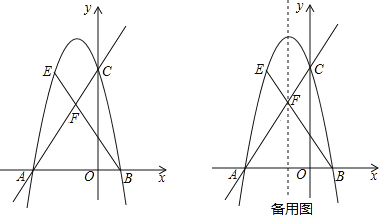
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求
时,求![]() 的值.
的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学六七年级有350名同学去春游,已知2辆A型车和1辆B型车可以载学生100人;1辆A型车和2辆B型车可以载学生110人.
(1)A、B型车每辆可分别载学生多少人?
(2)若租一辆A需要100元,一辆B需120元,请你设计租车方案,使得恰好运送完学生并且租车费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定“中小学生每天在校体育活动时间不低于1小时”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:
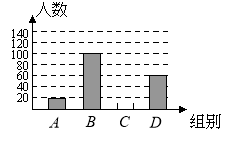
A组:![]() ;B组:
;B组:![]()
C组:![]() D组:
D组:![]()
请根据上述信息解答下列问题:
(1)C组的人数是;
(2)本次调查数据的中位数落在组内;
(3)若该辖区约有24 000名初中学生,请你估计其中达国家规定体育活动时间的人约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市16000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
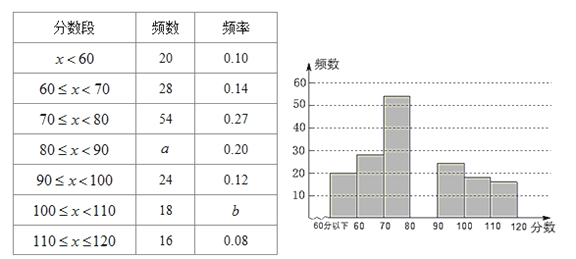
请根据以上图表提供的信息,解答下列问题:
(1)随机抽取部分学生的总人数是_________人,表格中的![]() _________.
_________.
(2)请补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市16000名九年级考生数学成绩为优秀的学生约有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com