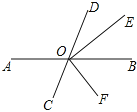
【题目】如图，直线AB交CD于点O，OE平分∠BOD，OF平分∠COB，∠AOD：∠BOE=4：1，则∠AOF等于（ ）
A. 
B. 
C. 
D. 
科目：初中数学 来源： 题型：
【题目】（1）如图①，在正方形
中，
、
分别是
、
边上的点，
，连接
，
交于点
．求证：
且
；
（2）如图②，若点、分别在
、
的延长线上，且，（1）中的结论是否成立？如果成立，请说明理由；
（3）如图③，在图②的基础上连接
、
、
、
、
、
分别是、、
、
的中点，请直接写出四边形
的形状．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】商场某种商品平均每天可销售30件，每件盈利50元。为了尽快减少库存，商场决定采取适当的降价措施。经调查发现，每件商品每降价1元，商场平均每天可多售出2件。设每件商品降价
元。据此规律，请回答：
（1）商场日销售量增加_____件，每件商品盈利_____元（用含
的代数式表示）。
（2）在上述条件不变、销售正常情况下，每件商品降价多少元时，商场日盈利可达到2100元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】4月22日是世界地球日，为了增强学生环保意识，某中学八年级举行了“环保知识竞赛”活动，为了了解本次竞赛情况，只抽取了部分学生的成绩（满分100分，得分均为正整数）进行统计，请你根据下面还未完成的频数分布表和频数分布直方图，解答下列问题：
分组 | 频数 | 频率 |
50.5～60.5 | 4 | 0.08 |
60.5～70.5 | 8 | 0.16 |
70.5～80.5 | 10 | 0.20 |
80.5～90.5 | 16 | 0.32 |
90.5～100.5 | a | b |
（1）a＝ b＝ ；
（2）补全频数分布直方图；
（3）该校八年级有500名学生，估计八年级学生中竞赛成绩高于80分的有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
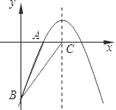
【题目】如图，已知二次函数y=﹣
+bx+c的图象经过A（2，0）、B（0，﹣6）两点．
（1）求这个二次函数的解析式；
（2）求当x满足什么条件时，函数值大于0？；
（3）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，直线y=x-3交x轴于点B，交y轴于点C，抛物线经过点A(-1，0)，B，C三点,点F在y轴负半轴上，OF=OA.
(1)求抛物线的解析式；
(2)在第一象限的抛物线上存在一点P，满足S△ABC=S△PBC，请求出点P的坐标；
(3)点D是直线BC的下方的抛物线上的一个动点，过D点作DE∥y轴，交直线BC于点E，①当四边形CDEF为平行四边形时，求D点的坐标；
②是否存在点D，使CE与DF互相垂直平分？若存在，请求出点D的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
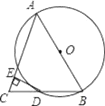
【题目】如图所示，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连接AC，过点D作DE⊥AC于E．
（1）求证：AB=AC；
（2）求证：DE为⊙O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，是用大小相等的小正方形按一定规律拼成的，则第10个图形是_________个小正方形，第n 个图形是___________个小正方形．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
