
【题目】如图,有一矩形纸片ABCD,AB=8,AD=17,将此矩形纸片折叠,使顶点A落在BC边的A′处,折痕所在直线同时经过边AB、AD(包括端点),设BA′=x,则x的取值范围是 .

【答案】![]()
【解析】
试题作出图形,根据矩形的对边相等可得BC=AD,CD=AB,当折痕经过点D时,根据翻折的性质可得A′D=AD,利用勾股定理列式求出A′C,再求出BA′;当折痕经过点B时,根据翻折的性质可得BA′=AB,此两种情况为BA′的最小值与最大值的情况,然后写出x的取值范围即可.
试题解析:
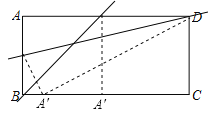
如图,∵四边形ABCD是矩形,AB=8,AD=17,
∴BC=AD=17,CD=AB=8,
①当折痕经过点D时,
由翻折的性质得,A′D=AD=17,在Rt△A′CD中,A′C=15 ∴BA′=BC-A′C=17-15=2;
②当折痕经过点B时,由翻折的性质得,BA′=AB=8,
∴x的取值范围是2≤x≤8.
故答案为:2≤x≤8.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
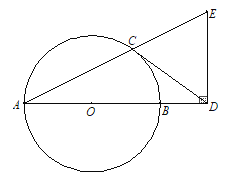
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB=12cm,点C在线段AB上,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB中点,求DE的长.
(2)若AC=4cm,求DE的长.
(3)若点C为线段AB上的一个动点(点C不与A,B重合),求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
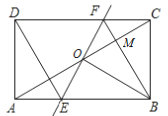
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.

(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的曲线是函数y=![]() (m为常数)图象的一支.
(m为常数)图象的一支.
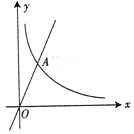
(1)求常数m的取值范围;
(2)若该函数的图象与正比例函数y=2x的图象在第一象限的交点为A(2,n),求点A的坐标及反比例
函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将若干枝铅笔分给甲、乙两个班级,甲班有一人分到6枝,其余的每人都分到13枝,乙班有一人分到5枝,其余的每人都分到10枝.如果分到两个班级的铅笔数目相同,并且大于100而不超过200那么甲、乙两个班各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
|
| 0.32 |
|
|
|
| 10 | 0.1 |
合计 | 100 | 1 |
书法作品比赛成绩频数直方图

根据上述信息,解答下列问题:
(1)请你把表中空白处的数据填写完整.
(2)请补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级的幅数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com