
分析 (1)根据题意可得$a-\frac{1}{a}=2$,再利用完全平方公式计算即可;
(2)根据倒数的定义和完全平方公式计算即可.
解答 解:(1)(2a+1)(1-2a)-(3-2a)2+9a2=14a-71-4a2-(9-12a+4a2)+9a2-14a+7=0,
整理得:a2-2a-1=0
∴$a-\frac{1}{a}=2$,
∴${a^2}+\frac{1}{a^2}={({a-\frac{1}{a}})^2}+2=4+2=6$;
(2)解:$\frac{a^2}{{5{a^4}+{a^2}+5}}$的倒数为$\frac{{5{a^4}+{a^2}+5}}{a^2}$,
∵$\frac{{5{a^4}+{a^2}+5}}{a^2}=5{a^2}+\frac{5}{a^2}+1=5({{a^2}+\frac{1}{a^2}})+1=5×6+1=31$,
∴$\frac{a^2}{{5{a^4}+{a^2}+5}}=\frac{1}{31}$.
点评 此题考查完全平方公式,关键是根据完全平方公式进行变形解答.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
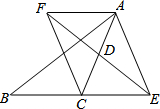 已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.
已知:如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连结AE,CF.试猜想线段AF与线段CE有何关系,并说明原因.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com