
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )

A. 12B. 24C. 12![]() D. 16
D. 16![]()
【答案】D
【解析】
在矩形ABCD中根据AD∥BC得出∠DEF=∠EFB=60°,由折叠的性质可得∠A=∠A′=90°,A′E=AE=2,AB=A′B′,∠A′EF=∠AEF=180°-60°=120°,∠A′EB′=60°.根据直角三角形的性质得出A′B′=AB=2![]() ,然后根据矩形的面积公式列式计算即可得解.
,然后根据矩形的面积公式列式计算即可得解.
在矩形ABCD中,
∵AD∥BC,
∴∠B′EF=∠EFB=60°,
由折叠的性质得∠A=∠A′=90°,A′E=AE=2,AB=A′B′,∠A′EF=∠AEF=180°-60°=120°,
∴∠A′EB′=∠A′EF-∠B′EF=120°-60°=60°.
在Rt△A′EB′中,
∵∠A′B′E=90°-60°=30°,
∴B′E=2A′E,而A′E=2,
∴B′E=4,
∴A′B′=2![]() ,即AB=2
,即AB=2![]() ,
,
∵AE=2,DE=6,
∴AD=AE+DE=2+6=8,
∴矩形ABCD的面积=ABAD=2![]() ×8=16
×8=16![]() .
.
故选:D.


科目:初中数学 来源: 题型:
【题目】同样大小的黑色棋子按图中所示的规律摆放:

(1)填写下表:
图形序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
图中棋子数 | 6 | 9 |
|
|
|
|
| … |
(2)照这样的方式摆下去,写出摆第n(n为正整数)个图形所需黑色棋子的颗数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲三角形的周长为![]() ,乙三角形的第一条边长为
,乙三角形的第一条边长为![]() ,第二条边长为
,第二条边长为![]() ,第三条边比第二条边短
,第三条边比第二条边短![]() .
.
(1)求乙三角形第三条边的长;
(2)甲、乙两三角形的周长哪个大?试说明理由;
(3)a、b都为正整数,甲、乙两三角形的周长在数轴上表示的点分别为A、B,若A、B两点之间恰好有18个“整数点”(点表示的数为整数),求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC,垂足为E.
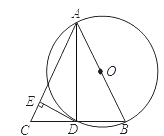
(1)求证:AB=AC;
(2)求证:DE为⊙O的切线;
(3)若⊙O半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
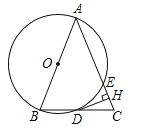
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC,AC分别交于D,E两点,过点D作DH⊥AC于点H.
(1)判断DH与⊙O的位置关系,并说明理由;
(2)求证:H为CE的中点;
(3)若BC=10,cosC=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,4张如图1的长为a,宽为b(a>b)长方形纸片,按图2的方式放置,阴影部分的面积为S1,空白部分的面积为S2,若S2=2S1,则a,b满足( )
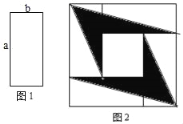
A. a=![]() B. a=2bC. a=
B. a=2bC. a=![]() bD. a=3b
bD. a=3b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果种植大户小芳,为了吸引更多的顾客,组织了观光采摘游活动,每一位来采摘水果的顾客都有一次抽奖机会,在一只不透明的盒子里有A(苹果),B(梨子),C(葡萄),D(葡萄)四张外形完全相同的卡片,抽奖时先随机抽取一张卡片,再从盒子中剩下的3张中随机抽取第二张.
(1)请利用树状图或列表的方法,表示前后两次抽得的卡片所有可能的情况;
(2)如果抽得的两张卡片是同一种水果图片就可获得奖励,那么得到奖励的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.

(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了宣传2018年世界杯,实现“足球进校园”的目标,任城区某中学计划为学校足球队购买一批足球,已知购买2个A品牌的足球和3个B品牌的足球共需380元;购买4个A品牌的足球和2个B品牌的足球共需360元.
(1)求A,B两种品牌的足球的单价.
(2)学校准备购进这两种品牌的足球共50个,并且B品牌足球的数量不少于A品牌足球数量的4倍,请设计出最省钱的购买方案,求该方案所需费用,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com