
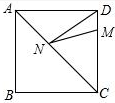
 在正方形ABCD中,AB=8,M是DC上的一点,且DM=2,N是AC上的一动点,求DN+MN的最小值与最大值.
在正方形ABCD中,AB=8,M是DC上的一点,且DM=2,N是AC上的一动点,求DN+MN的最小值与最大值. 分析 要求DN+MN的最小值,DN,MN不能直接求,可考虑通过作辅助线转化DN,MN的值,从而找出其最小值求解;当点N位于点A处是DN+MN有最大值.
解答 解:如图1,连接BM.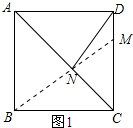
∵点B和点D关于直线AC对称,
∴NB=ND,
则BM就是DN+MN的最小值,
∵正方形ABCD的边长是8,DM=2,
∴CM=6,
∴BM=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴DN+MN的最小值是10.
如图2所示,当点N与点A重合时,DN+MN有最大值.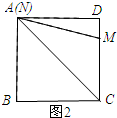
在Rt△NDM中,NM=$\sqrt{N{D}^{2}+D{M}^{2}}$=$\sqrt{{8}^{2}+{2}^{2}}$=2$\sqrt{17}$.
∴ND+NM=8+2$\sqrt{17}$.
点评 本题主要考查的是勾股定理的应用、轴对称路径最短问题,掌握DN+MN有最大值和最小值的条件是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2014x | B. | 2014x2 | C. | 2014x3 | D. | 672x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件赢利40元,为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加赢利,尽快减少库存.经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天销售这种童装赢利1200元,那么每件童装应降价多少元?
百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件赢利40元,为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加赢利,尽快减少库存.经市场调查发现:如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天销售这种童装赢利1200元,那么每件童装应降价多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com