
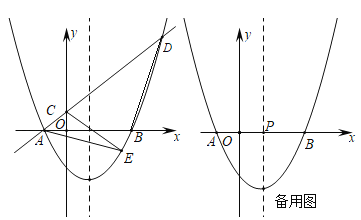
【题目】在平面直角坐标系中,将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与
的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,经过点
,经过点![]() 的一次函数
的一次函数![]() 的图象与
的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,且与抛物线的另一个交点为
,且与抛物线的另一个交点为![]() ,
,![]() 的面积为5.
的面积为5.
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点E的坐标;
面积的最大值,并求出此时点E的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 的面积最大值是
的面积最大值是![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ;(3)
;(3)![]() 的最小值是3.
的最小值是3.
【解析】
(1)先写出平移后的抛物线解析式,再把点![]() 代入可求得
代入可求得![]() 的值,由
的值,由![]() 的面积为5可求出点
的面积为5可求出点![]() 的纵坐标,代入抛物线解析式可求出横坐标,由
的纵坐标,代入抛物线解析式可求出横坐标,由![]() 、
、![]() 的坐标可利用待定系数法求出一次函数解析式;
的坐标可利用待定系数法求出一次函数解析式;
(2)作![]() 轴交
轴交![]() 于
于![]() ,如图,利用三角形面积公式,由
,如图,利用三角形面积公式,由![]() 构建关于E点横坐标的二次函数,然后利用二次函数的性质即可解决问题;
构建关于E点横坐标的二次函数,然后利用二次函数的性质即可解决问题;
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,则
,则![]() ,利用锐角三角函数的定义可得出
,利用锐角三角函数的定义可得出![]() ,此时
,此时![]() 最小,求出最小值即可.
最小,求出最小值即可.
解:(1)将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为
的图象向右平移1个单位,再向下平移2个单位,得到的抛物线解析式为![]() ,
,
∵![]() ,∴点
,∴点![]() 的坐标为
的坐标为![]() ,
,
代入抛物线的解析式得,![]() ,∴
,∴![]() ,
,
∴抛物线的解析式为![]() ,即
,即![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() 的面积为5,∴
的面积为5,∴![]() ,∴
,∴![]() ,
,
代入抛物线解析式得,![]() ,解得
,解得![]() ,
,![]() ,∴
,∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
∴ ,解得:
,解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)过点![]() 作
作![]() 轴交
轴交![]() 于
于![]() ,如图,设
,如图,设![]() ,则
,则![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() 的面积有最大值,最大值是
的面积有最大值,最大值是![]() ,此时
,此时![]() 点坐标为
点坐标为![]() .
.
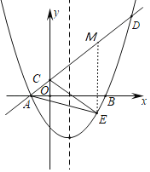
(3)作![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,∴
,∴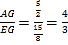 ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() 、
、![]() 关于
关于![]() 轴对称,∴
轴对称,∴![]() ,
,
∴![]() ,此时
,此时![]() 最小,
最小,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 的最小值是3.
的最小值是3.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】[问题发现]
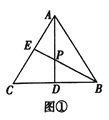
如图①,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,
上,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,则
,则![]() _____ ;
_____ ;
[拓展提高]
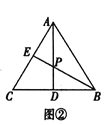
如图②,在等边三角形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 在边
在边![]() 上,直线
上,直线![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
[解决问题]
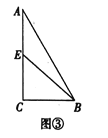
如图③,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,直线
上,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,![]() .请直接写出
.请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC是弦,沿BC对折劣弧BC,交AB于D,点E、F分别是弧AB和弧BD的中点.若AD=4,AB=10,则EF=_____.
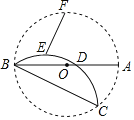
查看答案和解析>>
科目:初中数学 来源: 题型:
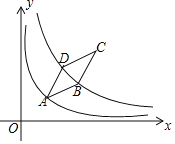
【题目】如图,菱形ABCD顶点A在函数y=![]() (x>0)的图像上,函数y=
(x>0)的图像上,函数y=![]() (k>4,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=4,∠ADC=150°,则k=______。
(k>4,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=4,∠ADC=150°,则k=______。
查看答案和解析>>
科目:初中数学 来源: 题型:
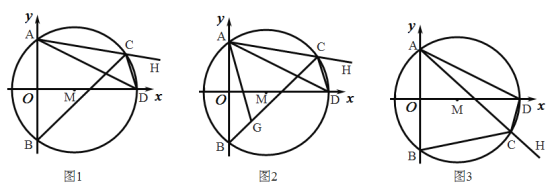
【题目】如图1,在平面直角坐标系中,已知![]() 的半径为5,圆心
的半径为5,圆心![]() 的坐标为
的坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是
是![]() 上的一点(不与点
上的一点(不与点![]() 、
、![]() 、
、![]() 重合),连结
重合),连结![]() 并延长,连结
并延长,连结![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)当点![]() 在
在![]() 上时.
上时.
①求证:![]() ;
;
②如图2,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连结
,连结![]() .求证:
.求证:![]() ;
;
(3)如图3,当点![]() 在
在![]() 上运动的过程中,试探究
上运动的过程中,试探究![]() 的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设函数y=x2+2kx+k﹣1(k为常数),下列说法正确的个数是( )
(1)对任意实数k,函数与x轴有两个交点
(2)当x≥﹣k时,函数y的值都随x的增大而增大
(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上
(4)对任意实数k,抛物线y=x2+2kx+k﹣1都必定经过唯一定点
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】黄山景区销售一种旅游纪念品,已知每件进价为![]() 元,当销售单价定为
元,当销售单价定为![]() 元时,每天可以销售
元时,每天可以销售![]() 件.市场调查反映:销售单价每提高
件.市场调查反映:销售单价每提高![]() 元,日销量将会减少
元,日销量将会减少![]() 件.物价部门规定:销售单价不低于
件.物价部门规定:销售单价不低于![]() 元,但不能超过
元,但不能超过![]() 元,设该纪念品的销售单价为
元,设该纪念品的销售单价为![]() (元),日销量为
(元),日销量为![]() (件).
(件).
(1)直接写出![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)求日销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)的函数关系式.并求当
(元)的函数关系式.并求当![]() 为何值时,日销售利润最大,最大利润是多少?
为何值时,日销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.8m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),他先测得留在墙壁上的影高为1.2m,又测得地面的影长为2.6m,请你帮她算一下,树高是( )
A.4.25mB.4.45mC.4.60mD.4.75m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com