
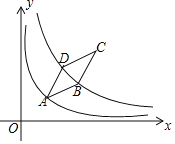
【题目】如图,菱形ABCD顶点A在函数y=![]() (x>0)的图像上,函数y=
(x>0)的图像上,函数y=![]() (k>4,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=4,∠ADC=150°,则k=______。
(k>4,x>0)的图象关于直线AC对称,且经过点B、D两点,若AB=4,∠ADC=150°,则k=______。
【答案】![]()
【解析】
连接OC,AC,过A作AE⊥x轴于点E,延长DA与x轴交于点F,过点D作DG⊥x轴于点G,得O、A、C在第一象限的角平分线上,求得A点坐标,进而求得D点坐标,便可求得结果.
连接OC,AC,过A作AE⊥x轴于点E,延长DA与x轴交于点F,过点D作DG⊥x轴于点G,
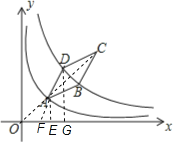
∵函数y=![]() (k>4,x>0)的图象关于直线AC对称,
(k>4,x>0)的图象关于直线AC对称,
∴O,A,C三点在同直线上,且∠COE=45°,
∴OE=AE,
不妨设OE=AE=a,则A(a,a),
∵点A在在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴a2=4,
∴a=±2(负值舍去),
∴a=2,
∴AE=OE=2,
∵四边形ABCD是菱形,∠ADC=150°,
∴∠BAD=30°,
∴∠OAF=∠CAD=![]() ∠BAD=15°,
∠BAD=15°,
∵∠OAE=∠AOE=45°,
∴∠EAF=30°,
∴AF=![]() =
=![]() ,EF=AEtan30°=
,EF=AEtan30°=![]() ,
,
∵AB=AD=4,AE∥DG,
∴![]() ,即
,即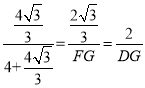
解得,FG=![]() ,DG=
,DG=![]()
∴EG=FG-FE=![]() -
-![]() =2,
=2,
∴OG=OE+EG=2+2=4,
∴D(4,![]() ),
),
∵D点D在函数y=![]() 的图象上,
的图象上,
∴k=4×(![]() )=8+8
)=8+8![]() .
.
故答案为:8+8![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
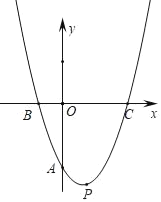
【题目】如图,在平面直角坐标系中,抛物线y=x(x﹣b)﹣![]() 与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
与y轴相交于A点,与x轴相交于B、C两点,且点C在点B的右侧,设抛物线的顶点为P.
(1)若点B与点C关于直线x=1对称,求b的值;
(2)若OB=OA,求△BCP的面积;
(3)当﹣1≤x≤1时,该抛物线上最高点与最低点纵坐标的差为h,求出h与b的关系;若h有最大值或最小值,直接写出这个最大值或最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系![]() 中有点
中有点![]() 和某一函数图象
和某一函数图象![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交图象
轴的垂线,交图象![]() 于点
于点![]() ,设点
,设点![]() ,
,![]() 的纵坐标分别为
的纵坐标分别为![]() ,
,![]() .如果
.如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的上位点;如果
的上位点;如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的图上点;如果
的图上点;如果![]() ,那么称点
,那么称点![]() 为图象
为图象![]() 的下位点.
的下位点.
(1)已知抛物线![]() .
.
① 在点A(-1,0),B(0,-2),C(2,3)中,是抛物线的上位点的是 ;
② 如果点![]() 是直线
是直线![]() 的图上点,且为抛物线的上位点,求点
的图上点,且为抛物线的上位点,求点![]() 的横坐标
的横坐标![]() 的取值范围;
的取值范围;
(2)将直线![]() 在直线
在直线![]() 下方的部分沿直线
下方的部分沿直线![]() 翻折,直线
翻折,直线![]() 的其余部分保持不变,得到一个新的图象,记作图象
的其余部分保持不变,得到一个新的图象,记作图象![]() .⊙
.⊙![]() 的圆心
的圆心![]() 在
在![]() 轴上,半径为
轴上,半径为![]() .如果在图象
.如果在图象![]() 和⊙
和⊙![]() 上分别存在点
上分别存在点![]() 和点F,使得线段EF上同时存在图象
和点F,使得线段EF上同时存在图象![]() 的上位点,图上点和下位点,求圆心
的上位点,图上点和下位点,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
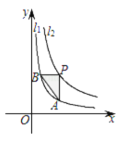
【题目】如图,函数![]() (x>0)和
(x>0)和![]() (x>0)的图象分别是
(x>0)的图象分别是![]() 和
和![]() .设点P在
.设点P在![]() 上,PA∥y轴交
上,PA∥y轴交![]() 于点A,PB∥x轴,交
于点A,PB∥x轴,交![]() 于点B,△PAB的面积为( )
于点B,△PAB的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知P为⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有点A、B(不与P、Q重合),连接AP、BP,若∠APQ=∠BPQ
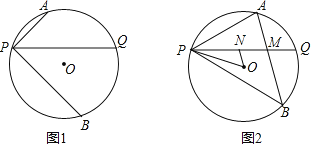
(1)如图1,当∠APQ=45°,AP=1,BP=2![]() 时,求⊙O的半径。
时,求⊙O的半径。
(2)如图2,连接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,设∠NOP=α,∠OPN=β,若AB平行于ON,探究α与β的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将二次函数![]() 的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与
的图象向右平移1个单位,再向下平移2个单位,得到如图所示的抛物线,该抛物线与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,经过点
,经过点![]() 的一次函数
的一次函数![]() 的图象与
的图象与![]() 轴正半轴交于点
轴正半轴交于点![]() ,且与抛物线的另一个交点为
,且与抛物线的另一个交点为![]() ,
,![]() 的面积为5.
的面积为5.
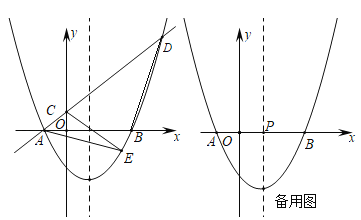
(1)求抛物线和一次函数的解析式;
(2)抛物线上的动点![]() 在一次函数的图象下方,求
在一次函数的图象下方,求![]() 面积的最大值,并求出此时点E的坐标;
面积的最大值,并求出此时点E的坐标;
(3)若点![]() 为
为![]() 轴上任意一点,在(2)的结论下,求
轴上任意一点,在(2)的结论下,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠ACD=90°,AC=DC,MN是过点A的直线,DB⊥MN于点B.

(1)如图,求证:BD+AB=![]() BC;
BC;
(2)直线MN绕点A旋转,在旋转过程中,当∠BCD=30°,BD=![]() 时,求BC的值.
时,求BC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初中英语口语听力考试即将举行,准备了A、B、C、D四份听力材料,它们的难易程度分别是易、中、难、难;另有a、b是两份口语材料,它们的难易程度分别是易、难.
(1)从四份听力材料中,任选一份是难的听力材料的概率是 ;
(2)用树状图形或列表法,求出听力、口语两份材料都是难的一套模拟试卷的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com