
【题目】如图,反比例函数![]() 的图象与直线
的图象与直线![]() 相交于
相交于![]() ,
,![]() ,点
,点![]() 是
是![]() 轴上一动点.
轴上一动点.
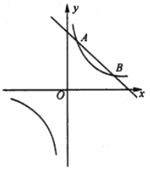
(1)①![]() _______;②当
_______;②当![]() 时,
时,![]() 的取值范围是_______;
的取值范围是_______;
(2)求反比例函数![]() 与直线
与直线![]() 的解析式;
的解析式;
(3)当![]() 是等腰三角形时,求点
是等腰三角形时,求点![]() 的坐标.
的坐标.
【答案】(1)①2;②![]() 或
或![]() ;(2)反比例函数的解析式为
;(2)反比例函数的解析式为![]() ,直线的解析式为
,直线的解析式为![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)①首先根据A,B两点都在反比例函数图象上列出一个关系m的方程,解方程即可求出m的值;
②根据m的值进而求出A,B两点的坐标,数形结合即可得出不等式的解集;
(2)分别将A,B两点坐标代入一次函数与反比例函数的解析式中即可得出答案;
(3)根据等腰三角形的定义,分三种情况:![]() ,
,![]() ,
,![]() 分别进行讨论即可.
分别进行讨论即可.
解:(1)①∵点![]() ,
,![]() 都在反比例函数
都在反比例函数![]() 图象上,
图象上,
∴![]()
解得![]() ;
;
②∵![]() ,
,
∴![]() ,
,![]() ,
,
数形结合可知当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
(2)∵点![]() 在反比例函数
在反比例函数![]() 图象上,
图象上,
∴![]() ,
,
∴反比例函数的解析式为![]() ;
;
∵点![]() ,
,![]() 在直线
在直线![]() 上,
上,
∴ ,解得
,解得
∴直线的解析式为![]() ;
;
(3)设点![]() ,则
,则![]() ,
,![]() ,
,![]()
①当![]() 时,
时,![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
②当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
③当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
综上所述,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
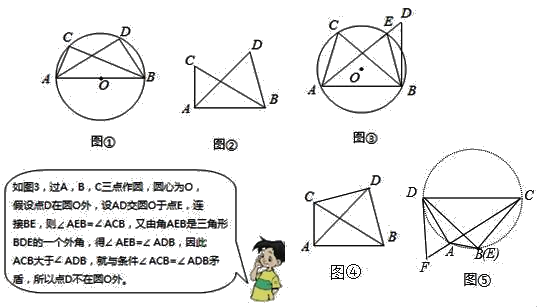
【题目】(发现)
如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①).
如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?请证明点D也不在⊙O内.
(应用)
利用(发现)和(思考)中的结论解决问题:
(1)如图④,已知∠BCD=∠BAD,∠CAD=40°,求∠CBD的度数.
(2)如图⑤,若四边形ABCD中,∠CAD=90°,作∠CDF=90°,交CA延长线于F,点E在AB上,∠AED=∠ADF,CD=3,EC=2,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的计算器,购进时的单价是20元,根据市场调查:在一段时间内,销售单价是30元时,销售量是600个,而销售单价每上涨1元,就会少售出10个.
(1)不妨设该种品牌计算器的销售单价为x元(x>30),请你分别用x的代数式来表示销售量y个和销售该品牌计算器获得利润w元,并把结果填写在表格中:
销售单价(元) | x(x>30) |
销售量y(个) |
|
销售计算器获得利润w(元) |
|
(2)在第(1)问的条件下,若计算器厂规定该品牌计算器销售单价不低于35元,且商场要完成不少于500个的销售任务,求:商场销售该品牌计算器获得最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 同时满足下列条件:①对称轴是
同时满足下列条件:①对称轴是![]() ;②最值是
;②最值是![]() ;③图象与
;③图象与![]() 轴有两个交点,其横坐标的平方和为
轴有两个交点,其横坐标的平方和为![]() ,则
,则![]() 的值是( )
的值是( )
A. 4或-30 B. -30 C. 4 D. 6或-20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)2x(2x+5)=(x﹣1)(2x+5) (2)x2+2x﹣5=0.
(3)x2﹣4x﹣1=0 (用公式法) (4)2x2+1=3x(用配方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
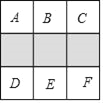
【题目】如图,在正方形方格中,阴影部分是涂黑3个小正方形所形成的图案.
(1)如果将一粒米随机地抛在这个正方形方格上,那么米粒落在阴影部分的概率是多少?
(2)现将方格内空白的小正方形(A,B,C,D,E,F)中任取2个涂黑,得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
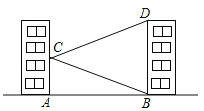
【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.
(1)求∠BCD的度数.
(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
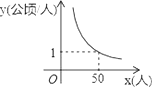
A. 该村人均耕地面积随总人口的增多而增多
B. 该村人均耕地面积y与总人口x成正比例
C. 若该村人均耕地面积为2公顷,则总人口有100人
D. 当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com