
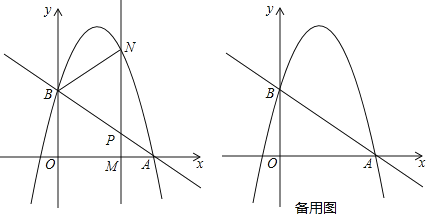
【题目】如图,直线y=kx+2与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求k的值和抛物线的解析式.
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,连接BN.
①若△BPN是直角三角形,求点N的坐标.
②当∠PBN=45°时,请直接写出m的值.(注:当k1k2=﹣1时,直线y=k1x+b1与直线y=k2x+b2垂直)
【答案】(1)k=﹣![]() , y=﹣
, y=﹣![]() x2+
x2+![]() x+2;(2)①点N(
x+2;(2)①点N(![]() ,
,![]() );②m=
);②m=![]() 或m=
或m=![]()
【解析】
(1)把![]() 点坐标代入直线解析式可求得
点坐标代入直线解析式可求得![]() ,则可求得
,则可求得![]() 点坐标,由
点坐标,由![]() 、
、![]() 的坐标,利用待定系数法可求得抛物线解析式;
的坐标,利用待定系数法可求得抛物线解析式;
(2)①分![]() 和
和![]() 两种情况讨论,即可求解;
两种情况讨论,即可求解;
②有两解,![]() 点在
点在![]() 的上方或下方,作辅助线,构建等腰直角三角形,由
的上方或下方,作辅助线,构建等腰直角三角形,由![]() 得
得![]() ,设
,设![]() ,则由
,则由![]() ,得
,得![]() ,
,![]() ,根据
,根据![]() ,可得
,可得![]() 和
和![]() 的解析式,分别与抛物线联立方程组,可得结论.
的解析式,分别与抛物线联立方程组,可得结论.
解:(1)把![]() 代入
代入![]() 中得,
中得,![]() ,
,
![]() ,
,
![]() 直线
直线![]() 的解析式为:
的解析式为:![]() ,
,
![]() ,
,
把![]() 和
和![]() 代入抛物线
代入抛物线![]() 中,
中,
则![]() ,
,
解得: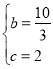 ,
,
二次函数的表达式为:![]() ;
;
(2)①当![]() 时,且
时,且![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 的纵坐标为2,
的纵坐标为2,
![]() ,
,
![]() (舍去),
(舍去),![]() ,
,
![]() 点
点![]() 坐标
坐标![]() ,
,![]() ;
;
当![]() 时,
时,
直线![]() 的解析式为:
的解析式为:![]() ,
,
![]()
![]() ,
,
![]() (舍去),
(舍去),![]() ,
,
![]() 点N(
点N(![]() ,
,![]() );
);
②有两解,![]() 点在
点在![]() 的上方或下方,
的上方或下方,
如图2,过点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() ,
,
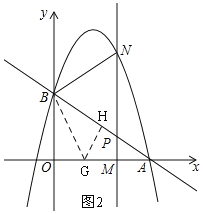
过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() .
.
由![]() 得
得![]() ,
,
![]() ,
,
设![]() ,则由
,则由![]() ,
,
![]()
![]() ,
,
得![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() ,
,
![]() ,
,
从而![]() ,
,
即![]() ,
,![]() ,
,
由![]() ,
,![]() ,
,![]() 得:
得:
直线![]() ,直线
,直线![]() .
.
则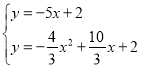 ,
,
解得:![]() (舍),
(舍),![]() ,
,
即![]() ;
;
则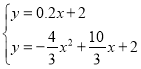 ,
,
解得:![]() (舍
(舍![]() ,
,![]() ;
;
即![]() ;
;
故![]() 与
与![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,是真命题的是( )
A.将函数y=![]() x+1向右平移2个单位后所得函数的解析式为y=
x+1向右平移2个单位后所得函数的解析式为y=![]() x
x
B.若一个数的平方根等于其本身,则这个数是0和1
C.对函数y=![]() ,其函数值y随自变量x的增大而增大
,其函数值y随自变量x的增大而增大
D.直线y=3x+1与直线y=﹣3x+2一定互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)点![]() 关于坐标原点
关于坐标原点![]() 对称的点的坐标为______;
对称的点的坐标为______;
(2)将![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,画出旋转后得到的
,画出旋转后得到的![]() ;
;
(3)在(2)中,求边![]() 所扫过区域的面积是多少?(结果保留
所扫过区域的面积是多少?(结果保留![]() ).
).
(4)若![]() 、
、![]() 、
、![]() 三点的横坐标都加3,纵坐标不变,图形
三点的横坐标都加3,纵坐标不变,图形![]() 的位置发生怎样的变化?
的位置发生怎样的变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个二次函数图象的顶点是![]() ,且与
,且与![]() 轴的交点的纵坐标为4.
轴的交点的纵坐标为4.
(1)求这个二次函数的表达式;
(2)当![]() 取哪些值时,
取哪些值时,![]() 的值随
的值随![]() 值的增大而增大?
值的增大而增大?
(3)点![]() 在这个二次函数的图象上吗?
在这个二次函数的图象上吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
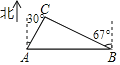
【题目】如图,从A城市到B城市要翻过一座大山,现需要打通隧道,修建高铁方便两地出行,已知在A城市的北偏东30°方向和B城市的北偏西67°方向有一C地,A,C相距230km,求A,B两个城市之间的距离.(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.7,结果精确到1km)
≈1.7,结果精确到1km)
查看答案和解析>>
科目:初中数学 来源: 题型:
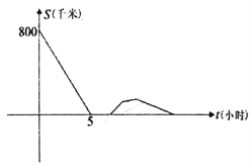
【题目】一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车相遇后都停下来休息,快车休息2个小时后,以原速的![]() 继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的
继续向甲行驶,慢车休息3小时后,接到紧急任务,以原速的![]() 返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
返回甲地,结果快车比慢车早2.25小时到达甲地,两车之间的距离S(千米)与慢车出发的时间t(小时)的函数图象如图所示,则当快车到达甲地时,慢车距乙地______千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点(1,0),且对称轴为直线
经过点(1,0),且对称轴为直线![]() ,其部分图象如图所示.对于此抛物线有如下四个结论:①
,其部分图象如图所示.对于此抛物线有如下四个结论:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确结论的序号是( )
时的函数值.其中正确结论的序号是( )
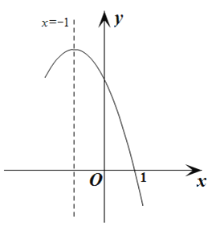
A.①③B.②④C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
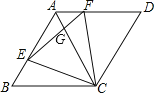
【题目】如图,菱形ABCD的边长为4,E,F分别是AB,AD边上的动点,BE=AF,∠BAD=120°,则下列结论:①△BEC≌△AFC;②△ECF为等边三角形;③∠AGE=∠AFC;④若AF=1,则![]() . 其中正确结论的序号有________.
. 其中正确结论的序号有________.
查看答案和解析>>
科目:初中数学 来源: 题型:
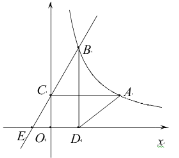
【题目】如图,已知反比例函数![]() 的图象经过点
的图象经过点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() .点
.点![]() 为反比例函数图象上的一动点,过点
为反比例函数图象上的一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() .直线
.直线![]() 与
与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
(1)求反比例函数的表达式;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)是否存在点![]() ,使得四边形
,使得四边形![]() 为平行四边形?若存在,请求出点
为平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com