
【题目】抛物线![]() 经过点(1,0),且对称轴为直线
经过点(1,0),且对称轴为直线![]() ,其部分图象如图所示.对于此抛物线有如下四个结论:①
,其部分图象如图所示.对于此抛物线有如下四个结论:①![]() <0; ②
<0; ②![]() ;③9a-3b+c=0;④若
;③9a-3b+c=0;④若![]() ,则
,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值.其中正确结论的序号是( )
时的函数值.其中正确结论的序号是( )
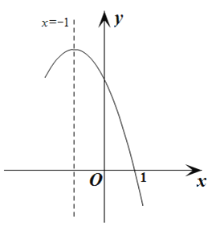
A.①③B.②④C.②③D.③④
【答案】D
【解析】
①根据抛物线开口方向、对称轴、与y轴的交点即可判断;
②根据抛物线的对称轴方程即可判断;
③根据抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1可得抛物线与x轴的另一个交点坐标为(﹣3,0),即可判断;
④根据m>n>0,得出m﹣1和n﹣1的大小及其与﹣1的关系,利用二次函数的性质即可判断.
解:①观察图象可知:
a<0,b<0,c>0,∴abc>0,
所以①错误;
②∵对称轴为直线x=﹣1,
即﹣![]() =﹣1,解得b=2a,即2a﹣b=0,
=﹣1,解得b=2a,即2a﹣b=0,
所以②错误;
③∵抛物线y=ax2+bx+c经过点(1,0),且对称轴为直线x=﹣1,
∴抛物线与x轴的另一个交点为(﹣3,0),
当a=﹣3时,y=0,即9a﹣3b+c=0,
所以③正确;
∵m>n>0,
∴m﹣1>n﹣1>﹣1,
由x>﹣1时,y随x的增大而减小知x=m﹣1时的函数值小于x=n﹣1时的函数值,故④正确;
故选:D.


科目:初中数学 来源: 题型:
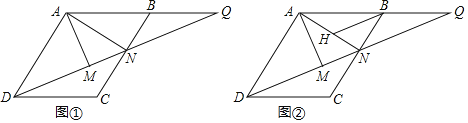
【题目】已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.
(1)如图①,若tan∠ADM=![]() ,MN=3,求BC的长;
,MN=3,求BC的长;
(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.
查看答案和解析>>
科目:初中数学 来源: 题型:
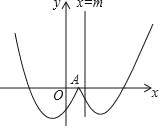
【题目】如图,在平面直角坐标系中,抛物线y=ax2﹣4ax+3(a≠0)与抛物线y=![]() +k均经过点A(1,0).直线x=m在这两条抛物线的对称轴之间(不与对称轴重合).函数y=ax2﹣4ax+3(x≥m)的图象记为G1,函数y=
+k均经过点A(1,0).直线x=m在这两条抛物线的对称轴之间(不与对称轴重合).函数y=ax2﹣4ax+3(x≥m)的图象记为G1,函数y=![]() +k(x≤m)的图象记为G2,图象G1与G2合起来得到的图形记为G.
+k(x≤m)的图象记为G2,图象G1与G2合起来得到的图形记为G.
(1)求a、k的值.
(2)当m=![]() 时,求图形G上y随x的增大而减小时x的取值范围.
时,求图形G上y随x的增大而减小时x的取值范围.
(3)当﹣2≤x≤![]() 时,图形G上最高点的纵坐标为2,求m的值.
时,图形G上最高点的纵坐标为2,求m的值.
(4)当直线y=2m﹣1与图形G有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
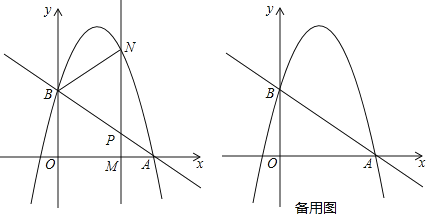
【题目】如图,直线y=kx+2与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A,B.
x2+bx+c经过点A,B.
(1)求k的值和抛物线的解析式.
(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,连接BN.
①若△BPN是直角三角形,求点N的坐标.
②当∠PBN=45°时,请直接写出m的值.(注:当k1k2=﹣1时,直线y=k1x+b1与直线y=k2x+b2垂直)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为引导学生广泛阅读文学名著,某校在七年级、八年级开展了读书知识竞赛,该校七、八年级各有学生![]() 人,各随机抽取
人,各随机抽取![]() 名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
名学生进行了抽样调查,获得了他们知识竞赛成绩(分),并对数据进行整理、描述和分析.下面给出了部分信息.
七年级:
![]()
八年级:
![]()
成绩人数 |
|
|
|
|
|
七年级 |
|
|
|
|
|
八年级 |
|
|
|
|
|
平均数、中位数、众数如表所示:
年级 | 平均数 | 中位数 | 众数 |
七年级 |
|
|
|
八年级 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]() ,
,![]() ,
,![]() _
_
![]() 该校对读书知识竞赛成绩不少于
该校对读书知识竞赛成绩不少于![]() 分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
分的学生授予“阅读小能手”称号,请你估计该校七、八年级所有学生中获得“阅读小能手”称号的大约有 人;
![]() 结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
结合以数据,你认为哪个年级读书知识竞赛的总体成绩较好,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,点A(0,2),正方形OABC的顶点B在函数![]() (k ≠ 0,x<0) 的图象上,直线
(k ≠ 0,x<0) 的图象上,直线![]() :
:![]() 与函数
与函数![]() (k ≠ 0,x<0) 的图象交于点D,与x轴交于点E.
(k ≠ 0,x<0) 的图象交于点D,与x轴交于点E.
(1)求k的值;
(2)横、纵坐标都是整数的点叫做整点.
①当一次函数![]() 的图象经过点A时,直接写出△DCE内的整点的坐标;
的图象经过点A时,直接写出△DCE内的整点的坐标;
②若△DCE内的整点个数恰有6个,结合图象,求b的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近些年全国各地频发雾霾天气,给人民群众的身体健康带来了危害,某商场看到商机后决定购进甲、乙两种空气净化器进行销售.若每台甲种空气净化器的进价比每台乙种空气净化器的进价少300元,且用6000元购进甲种空气净化器的数量与用7500元购进乙种空气净化器的数量相同.
(1)求每台甲种空气净化器、每台乙种空气净化器的进价分别为多少元?
(2)若该商场准备进货甲、乙两种空气净化器共30台,且进货花费不超过42000元,问最少进货甲种空气净化器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年5月的第二个星期日即为母亲节,“父母恩深重,恩怜无歇时”,许多市民喜欢在母亲节为母亲送花,感恩母亲,祝福母亲.今年节日前夕,某花店采购了一批鲜花礼盒,经分析上一年的销售情况,发现该鲜花礼盒的该周销售量y(盒)是销售单价x(元)的一次函数,已知销售单价为70元/盒时,销售量为160盒;销售单价为80元/盒时,销售量为140盒.
(1)求该周销售量y(盒)关于销售单价x(元)的一次函数解析式;
(2)若按去年方式销售,已知今年该鲜花礼盒的进价是每盒50元,商家要求该周至少要卖110盒,请你帮店长算一算,要完成商家的销售任务,销售单价不能超过多少元?
(3)在(2)的条件下,试确定销售单价x为何值时,花店该周销售鲜花礼盒获得的利润最大?并求出获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com