
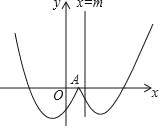
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y��ax2��4ax+3��a��0����������y��![]() +k��������A��1��0����ֱ��x��m�������������ߵĶԳ���֮�䣨����Գ����غϣ�������y��ax2��4ax+3��x��m����ͼ���ΪG1������y��
+k��������A��1��0����ֱ��x��m�������������ߵĶԳ���֮�䣨����Գ����غϣ�������y��ax2��4ax+3��x��m����ͼ���ΪG1������y��![]() +k��x��m����ͼ���ΪG2��ͼ��G1��G2�������õ���ͼ�μ�ΪG��
+k��x��m����ͼ���ΪG2��ͼ��G1��G2�������õ���ͼ�μ�ΪG��
��1����a��k��ֵ��
��2����m��![]() ʱ����ͼ��G��y��x���������Сʱx��ȡֵ��Χ��
ʱ����ͼ��G��y��x���������Сʱx��ȡֵ��Χ��
��3������2��x��![]() ʱ��ͼ��G����ߵ��������Ϊ2����m��ֵ��
ʱ��ͼ��G����ߵ��������Ϊ2����m��ֵ��
��4����ֱ��y��2m��1��ͼ��G��2��������ʱ��ֱ��д��m��ȡֵ��Χ��
���𰸡���1��a��1��k����2����2��x����1��![]() ��x��2����3��m��2��
��x��2����3��m��2��![]() ��m=��1+2
��m=��1+2![]() ����4����
����4����![]() ��m��1��
��m��1��![]() ��m��0��3��
��m��0��3��![]() ��m��1+
��m��1+![]() ��
��
��������
��1����A���������������������ʽ�У������ô���ϵ��a��k��
��2�������������������ͼ��Ϻ���ͼ����⣻
��3����m�����������ͼ���ۣ�
��4����������Ҫ��ͼ�ҵ��ĸ��ٽ�㣬���ͼ����⣮
�⣺��1����������y��ax2��4ax+3��a��0����������y��![]() +kͼ��G1���������A��1��0��
+kͼ��G1���������A��1��0��
��a��4a+3��0��![]() ��22+k��0��
��22+k��0��
���a��1��k����2��
��2����y��x2��4x+3����x��2��2��1��
��ͼ��G1��ĶԳ���Ϊֱ��x��2��
��y��![]() ��2����ͼ��G2��ĶԳ���Ϊֱ��x����1��
��2����ͼ��G2��ĶԳ���Ϊֱ��x����1��
�൱m��![]() ʱ��ͼ��G��y��x���������Сʱx��ȡֵ��Χ��x����1��
ʱ��ͼ��G��y��x���������Сʱx��ȡֵ��Χ��x����1��![]() ��x��2��
��x��2��
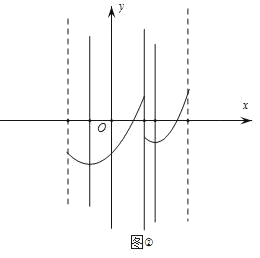
��3������1��m��1ʱ��m2��4m+3��2 ����ͼ1��
���m1��2��![]() ��m2��2+
��m2��2+![]() ��1����ȥ��
��1����ȥ��
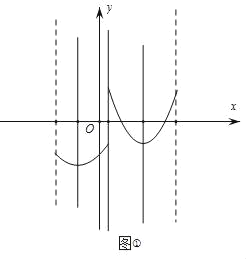
��1��m��2ʱ��![]() ��m+1��2��2��2 ����ͼ2��
��m+1��2��2��2 ����ͼ2��
���m1����1+2![]() ��m2����1��2
��m2����1��2![]() ��1����ȥ��
��1����ȥ��
��4����ֱ��y��2m��1��y����x��2��2��1��x��m�ཻʱ��
2m��1����m��2��2��1��
��m��3+![]() ��m��3��
��m��3��![]() ��
��
��ֱ��y��2m��1��y��![]() ��2��x��m�ཻʱ��
��2��x��m�ཻʱ��
2m��1��![]() ��2
��2
��m��1+![]() ��m��1��
��m��1��![]() ��
��
��y��2m��1����2ʱ��m����![]() ��
��
��y��2m��1����1ʱ��m��0��
�ੁ![]() ��m��1��
��m��1��![]() ��m��0��3��
��m��0��3��![]() ��m��1+
��m��1+![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
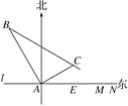
����Ŀ����ij�ɻ�����������ĵ���l����һ��Ϊ1 km�ķɻ��ܵ�MN(��ͼ)�����ܵ�MN��������14.5ǧ�״���һ�۲�վA.ijʱ�̲��һ������ֱ�߽���ķɻ�λ�ڵ�A�ı�ƫ��30���������A���15ǧ��B��������1���ӣ��ֲ�ø÷ɻ�λ�ڵ�A�ı�ƫ��60���������A���5![]() ǧ��C����
ǧ��C����
(1)�÷ɻ����е��ٶ��Ƕ���ǧ��/Сʱ��(�����������)
(2)����÷ɻ����ı亽��������У���ô�ɻ��ܷ������ܵ�MN֮�䣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��5G�����ǵ�����ƶ�ͨ�����磬�����ƶ��ҹ����־��÷�չ������̨��. ��Ԥ�⣬2020�굽2030���й�5Gֱ�Ӿ��ò����ͼ�Ӿ��ò������������ͼ��ʾ.
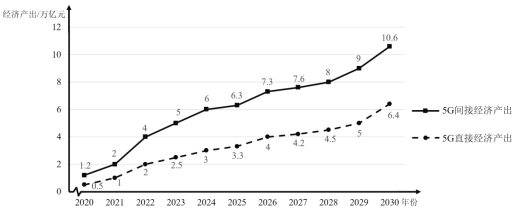
������ͼ�ṩ����Ϣ�������ƶϲ��������ǣ� ��
A.2030��5G��Ӿ��ò�����5Gֱ�Ӿ��ò�����4.2����Ԫ
B.2020�굽2030�꣬5Gֱ�Ӿ��ò�����5G��Ӿ��ò���������������
C.2030��5Gֱ�Ӿ��ò���ԼΪ2020��5Gֱ�Ӿ��ò�����13��
D.2022�굽2023����2023�굽2024��5G��Ӿ��ò�������������ͬ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��������������ֱ�Ϊ
��������������ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��
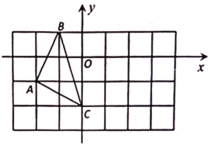
��1����![]() ��������ԭ��
��������ԭ��![]() �ԳƵĵ������Ϊ______��
�ԳƵĵ������Ϊ______��
��2����![]() ���ŵ�
���ŵ�![]() ˳ʱ����ת
˳ʱ����ת![]() ��������ת��õ���
��������ת��õ���![]() ��
��
��3���ڣ�2���У����![]() ��ɨ�����������Ƕ��٣����������
��ɨ�����������Ƕ��٣����������![]() ����
����
��4����![]() ��
��![]() ��
��![]() ����ĺ����궼��3�������겻�䣬ͼ��
����ĺ����궼��3�������겻�䣬ͼ��![]() ��λ�÷��������ı仯��
��λ�÷��������ı仯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
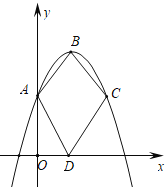
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y����x2+3x+2��y�ύ�ڵ�A����B�������ߵĶ��㣬��C���A���������Ϲ��ڶԳ���ԳƵ������㣬��D��x�����˶������ı���ABCD�������Խ��ߵij���֮�͵���СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����κ���ͼ��Ķ�����![]() ������
������![]() ��Ľ����������Ϊ4��
��Ľ����������Ϊ4��
��1����������κ����ı���ʽ��
��2����![]() ȡ��Щֵʱ��
ȡ��Щֵʱ��![]() ��ֵ��
��ֵ��![]() ֵ�����������
ֵ�����������
��3����![]() ��������κ�����ͼ������
��������κ�����ͼ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
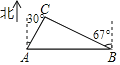
����Ŀ����ͼ����A���е�B����Ҫ����һ����ɽ������Ҫ��ͨ�������������������س��У���֪��A���еı�ƫ��30�㷽���B���еı�ƫ��67�㷽����һC�أ�A��C���230km����A��B��������֮��ľ��룮���ο����ݣ�sin67���![]() ��cos67���
��cos67���![]() ��tan67���
��tan67���![]() ��
��![]() ��1.7�������ȷ��1km��
��1.7�������ȷ��1km��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ������(1��0)���ҶԳ���Ϊֱ��
������(1��0)���ҶԳ���Ϊֱ��![]() ���䲿��ͼ����ͼ��ʾ�����ڴ��������������ĸ����ۣ���
���䲿��ͼ����ͼ��ʾ�����ڴ��������������ĸ����ۣ���![]() ��0�� ��
��0�� ��![]() ����9a-3b+c=0������
����9a-3b+c=0������![]() ����
����![]() ʱ�ĺ���ֵС��
ʱ�ĺ���ֵС��![]() ʱ�ĺ���ֵ��������ȷ���۵�����ǣ� ��
ʱ�ĺ���ֵ��������ȷ���۵�����ǣ� ��
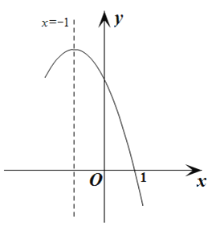
A.�٢�B.�ڢ�C.�ڢ�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�١�ͼ�ھ���4��4������������ÿ��С�����εĶ����Ϊ��㣬�ı���ABCD�Ķ�����ڸ���ϣ������̶�ֱ�ߣ��ֱ�����Ҫ��ͼ��
��1����ͼ���е��߶�CD���ҵ�һ��E������AE��ʹ��AE���ı���ABCD������ֳ�1:2�����֣�
��2����ͼ���е��ı���ABCD�ⲿ��һ��ֱ��l��ʹ��ֱ��l������һ�����A��B���������ε�������ı���ABCD�����![]() ����������ͼ�ۼ���
����������ͼ�ۼ���
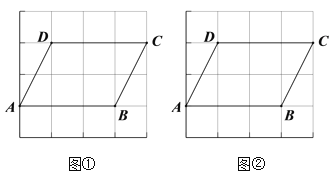
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com