
【题目】如图①,定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫作互补等对边四边形.如图②,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形.试说明:∠ABD=∠BAC=![]() ∠E.
∠E.

【答案】证明见解析.
【解析】
已知AE=BE,根据等腰三角形的性质可得∠EAB=∠EBA.根据互补等对边四边形的定义可得AD=BC.利用SAS证明△ABD≌△BAC,根据全等三角形的性质可得∠ABD=∠BAC,∠ADB=∠BCA;根据互补等对边四边形的定义可得∠ADB+∠BCA=180°,即可求得∠ADB=∠BCA=90°.在等腰△ABE中,根据等腰三角形的性质及三角形的内角和定理可得∠EAB=∠EBA=![]() (180°-∠E)=90°-
(180°-∠E)=90°-![]() ∠E,所以∠ABD=90°-∠EAB=90°-
∠E,所以∠ABD=90°-∠EAB=90°-![]() =
=![]() ∠E,由此即可证得结论.
∠E,由此即可证得结论.
∵AE=BE,
∴∠EAB=∠EBA.
∵四边形ABCD是互补等对边四边形,
∴AD=BC.
在△ABD与△BAC中,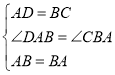 ,
,
∴△ABD≌△BAC,
∴∠ABD=∠BAC,∠ADB=∠BCA.
∵∠ADB+∠BCA=180°,
∴∠ADB=∠BCA=90°.
在等腰△ABE中,∵∠EAB=∠EBA=![]() (180°-∠E)=90°-
(180°-∠E)=90°-![]() ∠E,
∠E,
∴∠ABD=90°-∠EAB=90°-![]() =
=![]() ∠E,
∠E,
∴∠ABD=∠BAC=![]() ∠E.
∠E.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD平分∠ACB交AB于点D,E为AC上一点,且DE∥BC

(1)求证:DE=CE;
(2)若∠A=90°,S△BCD=26,BC=13,求AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF.
(1)求证:AD平分∠BAC;
(2)直接写出AB+AC与AE之间的等量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】6月14日是“世界献血日”,某市采取自愿报名的方式组织市民义务献血.献血时要对献血者的血型进行检测,检测结果有“A型”、“B型”、“AB型”、“O型”4种类型.在献血者人群中,随机抽取了部分献血者的血型结果进行统计,并根据这个统计结果制作了两幅不完整的图表:
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
(1)这次随机抽取的献血者人数为 人,m= ;
(2)补全上表中的数据;
(3)若这次活动中该市有3000人义务献血,请你根据抽样结果回答:
从献血者人群中任抽取一人,其血型是A型的概率是多少?并估计这3000人中大约有多少人是A型血?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F.
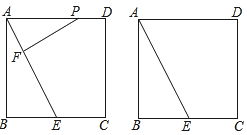
(1)求证:△PFA∽△ABE;
(2)当点P在射线AD上运动时,设PA=x,是否存在实数x,使以P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )
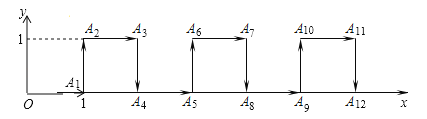
A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,以AB为直径的⊙O交AC于点D.过点C作CF∥AB,在CF上取一点E,使DE=CD,连接AE.对于下列结论:①AD=DC;②△CBA∽△CDE;③![]() =
=![]() ;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )
;④AE为⊙O的切线,一定正确的结论全部包含其中的选项是( )

A. ①② B. ①②③ C. ①④ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com