Question

【题目】如图，正方形ABCD的边长为4，E是BC边的中点，点P在射线AD上，过P作PF⊥AE于F．

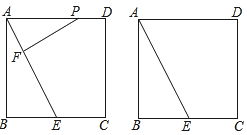
（1）求证：△PFA∽△ABE；

（2）当点P在射线AD上运动时，设PA=x，是否存在实数x，使以P，F，E为顶点的三角形也与△ABE相似？若存在，请求出x的值；若不存在，说明理由．

Answer 1

【答案】（1）证明见解析（2）2或5

【解析】

（1）在△PFA与△ABE中，易得∠PAF=∠AEB及∠PFA=∠ABE=90°；故可得△PFA∽△ABE；

（2）根据题意：若△EFP∽△ABE，则∠PEF=∠EAB；必须有PE∥AB；分两种情况进而列出关系式．

（1）证明：∵AD∥BC，

∴∠PAF=∠AEB．

∵∠PFA=∠ABE=90°，

∴△PFA∽△ABE．

（2）若△EFP∽△ABE，则∠PEF=∠EAB．

∴PE∥AB．

∴四边形ABEP为矩形．

∴PA=EB=2，即x=2．

若△PFE∽△ABE，则∠PEF=∠AEB．

∵∠PAF=∠AEB，

∴∠PEF=∠PAF．

∴PE=PA．

∵PF⊥AE，

∴点F为AE的中点．

∵AE=，

∴EF=AE=．

∵，即，

∴PE=5，即x=5．

∴满足条件的x的值为2或5．