
【题目】如图,AB是⊙O的直径,C是⊙0上的一点,直线MN经过点C,过点A作直线MN的垂线,垂足为点D,且∠BAC=∠DAC
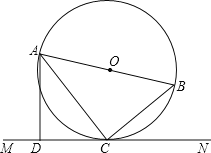
(1)猜想直线MN与⊙O的位置关系,并说明理由;
(2)若CD=6,cos∠ACD=![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)相切,理由见解析;(2)6.25
【解析】
(1)连接OC,推出AD∥OC,从而得OC⊥MN,根据切线的判定推出即可.
(2)求出AD、AB长,证△ADC∽△ACB,得出比例式,代入求出AB长即可.
解:(1)直线MN与⊙O的位置关系是相切.理由如下:
连接OC,
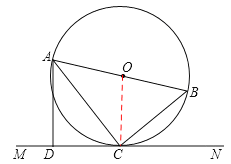
∵OA=OC,
∴∠OAC=∠OCA,
∵∠CAB=∠DAC,
∴∠DAC=∠OCA.
∴OC∥AD.
∵AD⊥MN,
∴OC⊥MN.
∵OC为半径,
∴MN是⊙O切线.
(2)∵CD=6,![]() ,
,
∴AC=10.
由勾股定理得:AD=8.
∵AB是⊙O直径,AD⊥MN,
∴∠ACB=∠ADC=90°.
∵∠DAC=∠BAC,
∴△ADC∽△ACB.
∴![]() ,即
,即![]() .
.
∴AB=12.5.
∴⊙O半径是![]() ×12.5=6.25.
×12.5=6.25.


科目:初中数学 来源: 题型:
【题目】学校打算用长![]() 米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为
米的篱笆围城一个长方形的生物园饲养小兔,生物园的一面靠在长为![]() 米的墙上(如图).
米的墙上(如图).

(1)若生物园的面积为![]() 平方米,求生物园的长和宽;
平方米,求生物园的长和宽;
(2)能否围城面积为![]() 平方米的生物园?若能,求出长和宽;若不能,请说明理由.
平方米的生物园?若能,求出长和宽;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学解一元二次方程x2﹣6x﹣1=0的过程如图所示.
解:x2﹣6x=1 …①
x2﹣6x+9=1 …②
(x﹣3)2=1 …③
x﹣3=±1 …④
x1=4,x2=2 …⑤
(1)小明解方程的方法是 .
(A)直接开平方法 (B)因式分解法 (C)配方法 (D)公式法
他的求解过程从第 步开始出现错误.
(2)解这个方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() .动点
.动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,沿射线
同时出发,沿射线![]() 、线段
、线段![]() 向点
向点![]() 的方向运动(点
的方向运动(点![]() 可运动到
可运动到![]() 的延长线上),当动点
的延长线上),当动点![]() 运动到点
运动到点![]() 时,
时,![]() 、
、![]() 两点同时停止运动.联结
两点同时停止运动.联结![]() 、
、![]() 、
、![]() ,过
,过![]() 三边的中点作
三边的中点作![]() .设动点
.设动点![]() 、
、![]() 的速度都是1个单位/秒,
的速度都是1个单位/秒,![]() 、
、![]() 运动的时间为
运动的时间为![]() 秒.试解答下列问题:
秒.试解答下列问题:
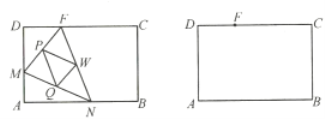
(1)说明![]() ;
;
(2)设![]() ,试问
,试问![]() 为何值时,
为何值时,![]() 为直角三角形?
为直角三角形?
(3)试用含![]() 的代数式表示
的代数式表示![]() ,并求当
,并求当![]() 为何值时,
为何值时,![]() 最小?求此时
最小?求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
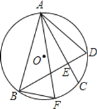
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AC=nAB,∠CAB=α,点E,F分别在AB,AC上且EF∥BC,把△AEF绕点A顺时针旋转到如图2的位置.连接CF,BE.

(1)求证:∠ACF=∠ABE;
(2)若点M,N分别是EF,BC的中点,当α=90°时,求证:BE2+CF2=4MN2;
(3)如图3,点M,N分别在EF,BC上且![]() =
=![]() =
=![]() ,若n=
,若n=![]() ,α=135°,BE=
,α=135°,BE=![]() ,直接写出MN的长.
,直接写出MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两家公司员工日工资情况:甲公司日工资是底薪100元,每完成一件产品工资计3元;乙公司无底薪,40件以内(含40件)产品的部分每件产品工资计8元,超出40件的部分每件产品工资计10元,为此,在这两家公司各随机调查了100名工人日完成产品数,并整理得到如下频数分布表:
日完成产品数 | 38 | 39 | 40 | 41 | 42 |
甲公司工人数 | 20 | 40 | 20 | 10 | 10 |
乙公司工人数 | 10 | 20 | 20 | 40 | 10 |
(1)若甲、乙公司日工资加上其他福利,总的待遇相同,A、B两人分别到甲、乙公司应聘,都选中甲公司的概率是多少?
(2)试以这两家公司各100名工人日工资的平均数作为决策依据,若某人要去这两家公司应聘,为他做出选择,去哪一家公司的经济收入可能会多一些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
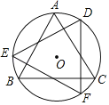
A.150°B.135°C.120°D.105°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com